
Zadanie Rozkłady dwójkowe (roz)
Pomóż nam usprawnić bazę zadań!
Rozkłady dwójkowe
Rozkładem dwójkowym liczby  nazywamy ciąg "cyfr"
nazywamy ciąg "cyfr" 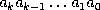 , taki że
, taki że
- każda z cyfr
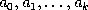 jest równa
jest równa 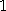 ,
, 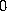 lub
lub 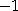 ;
; - najbardziej znacząca cyfra w rozkładzie, czyli
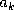 , jest różna od zera;
, jest różna od zera; 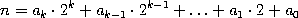 .
.
Można łatwo zauważyć, że liczba może mieć wiele różnych rozkładów dwójkowych.
Spośród tych wszystkich rozkładów, optymalnymi nazwiemy te, które mają najmniejszą liczbę cyfr niezerowych.
Na przykład, rozkładami dwójkowymi liczby 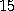 są: 10001, 1111 i 10011
(dla wygody cyfrę
są: 10001, 1111 i 10011
(dla wygody cyfrę 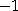 oznaczyliśmy tu jako 1).
Pierwszy z tych rozkładów jest rozkładem optymalnym dla
oznaczyliśmy tu jako 1).
Pierwszy z tych rozkładów jest rozkładem optymalnym dla 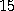 .
.
Zadanie
Twoim zadaniem jest napisanie programu, który obliczy, jaka jest liczba cyfr niezerowych w optymalnym rozkładzie dwójkowym podanej liczby.
Wejście
Program powinien czytać dane ze standardowego wejścia.
W pierwszym wierszu danych podana jest liczba  (
(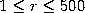 ).
W drugim wierszu podana jest liczba dziesiętna
).
W drugim wierszu podana jest liczba dziesiętna  złożona z
złożona z  cyfr.
Liczba
cyfr.
Liczba  jest zapisana począwszy od najbardziej znaczących cyfr (tzn.
tradycyjnie) i rozpoczyna się od cyfry różnej od zera.
jest zapisana począwszy od najbardziej znaczących cyfr (tzn.
tradycyjnie) i rozpoczyna się od cyfry różnej od zera.
Wyjście
Program powinien pisać wynik na wyjście standardowe.
Wynikiem powinna być liczba oznaczająca liczbę cyfr niezerowych w optymalnym rozkładzie dwójkowym liczby  .
.
Przykład
Dla danych wejściowych:
2 15
poprawną odpowiedzią jest:
2
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English