
Zadanie Wielokąty (wie)
Pomóż nam usprawnić bazę zadań!
Wielokąt
Limit pamięci: 32 MB
Dany jest  -kąt wypukły
-kąt wypukły 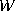 (gdzie
(gdzie 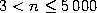 ) i
) i 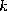 jego różnych przekątnych, parami nie
przecinających się wewnątrz wielokąta. (Jedynym wspólnym punktem dwóch różnych
przekątnych może być tylko wierzchołek wielokąta.) Wierzchołki wielokąta są
ponumerowane kolejno od
jego różnych przekątnych, parami nie
przecinających się wewnątrz wielokąta. (Jedynym wspólnym punktem dwóch różnych
przekątnych może być tylko wierzchołek wielokąta.) Wierzchołki wielokąta są
ponumerowane kolejno od 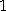 do
do  w kierunku przeciwnym do
ruchu wskazówek zegara. Wszystkie przekątne dzielą
w kierunku przeciwnym do
ruchu wskazówek zegara. Wszystkie przekątne dzielą  na mniejsze
wielokąty wypukłe o rozłącznych wnętrzach.
na mniejsze
wielokąty wypukłe o rozłącznych wnętrzach.
Przykład
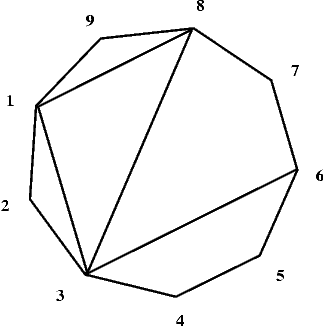
Cztery przekątne 1-8, 8-3, 3-1 i 3-6 dzielą wielokąt  przedstawiony
na poniższym rysunku na dwa czworokąty i trzy trójkąty.
przedstawiony
na poniższym rysunku na dwa czworokąty i trzy trójkąty.
Zadanie
Ułóż program, który:
- wczytuje opis wielokąta
 i jego przekątnych ze standardowego
wejścia;
i jego przekątnych ze standardowego
wejścia; - oblicza maksymalną liczbę boków wielokąta wśród wielokątów wypukłych
powstałych z podziału
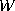 ;
; - zapisuje wynik w standardowym wyjściu.
Wejście
W każdym wierszu standardowego wejścia są zapisane dwie liczby całkowite dodatnie oddzielone pojedynczym odstępem.
W pierwszym wierszu jest zapisana liczba wierzchołków wielokąta  i
liczba przekątnych
i
liczba przekątnych 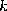 .
.
W każdym z kolejnych 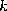 wierszy znajduje się opis jednej przekątnej
wielokąta w postaci pary liczb całkowitych dodatnich - numerów wierzchołków,
które łączy ta przekątna; bezpośrednio po drugiej z liczb następuje koniec
wiersza.
wierszy znajduje się opis jednej przekątnej
wielokąta w postaci pary liczb całkowitych dodatnich - numerów wierzchołków,
które łączy ta przekątna; bezpośrednio po drugiej z liczb następuje koniec
wiersza.
Dane w standardowym wejściu są zapisane poprawnie i Twój program nie musi tego sprawdzać.
Wyjście
W standardowym wyjściu należy zapisać jedną liczbę całkowitą dodatnią -
maksymalną liczbę boków wielokąta wypukłego powstałego z podziału danego
wielokąta 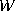 .
.
Przykład
Dla danych wejściowych:
9 4 1 8 8 3 3 1 3 6
poprawną odpowiedzią jest:
4
Autor zadania: Krzysztof Diks.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English