
Zadanie Trójramienny dźwig (tro)
Pomóż nam usprawnić bazę zadań!
Trójramienny dźwig
Limit pamięci: 32 MB
Trójramienny dźwig ustawia kontenery na wagonach kolejowych.
Wagony są ponumerowane kolejno 1, 2, ....
Na każdym wagonie można postawić co najwyżej jeden kontener.
W jednym ruchu dźwig pobiera ze składowiska trzy kontenery i
ustawia je na wagonach o numerach 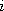 ,
,  oraz
oraz 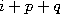 , albo
na wagonach o numerach
, albo
na wagonach o numerach 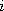 ,
, 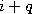 oraz
oraz 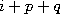 (dla pewnych stałych
(dla pewnych stałych 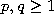 ).
Dźwig trzeba zaprogramować tak, żeby załadował kontenerami
pierwsze
).
Dźwig trzeba zaprogramować tak, żeby załadował kontenerami
pierwsze  wagonów pociągu (pociąg ma
wagonów pociągu (pociąg ma 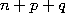 wagonów).
Program składa się z ciągu instrukcji.
Każda z instrukcji opisuje jeden ruch dźwigu.
Instrukcja programu ma postać trójki
wagonów).
Program składa się z ciągu instrukcji.
Każda z instrukcji opisuje jeden ruch dźwigu.
Instrukcja programu ma postać trójki 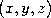 , gdzie
, gdzie
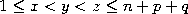 , i określa numery wagonów, na które
dźwig ma ustawić kontenery.
Jeżeli po wykonaniu programu na każdym spośród
, i określa numery wagonów, na które
dźwig ma ustawić kontenery.
Jeżeli po wykonaniu programu na każdym spośród  pierwszych
wagonów pociągu znajduje się dokładnie jeden kontener, to mówimy,
że program jest poprawny.
pierwszych
wagonów pociągu znajduje się dokładnie jeden kontener, to mówimy,
że program jest poprawny.
Zadanie
Napisz program, który:
- ze standardowego wejścia wczyta charakterystykę dźwigu
(liczby
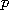 i
i 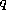 ) oraz liczbę wagonów do załadowania (
) oraz liczbę wagonów do załadowania ( ),
),
- wygeneruje poprawny program dla dźwigu,
- wypisze go na standardowe wyjście.
Wejście
W pierwszym i jedynym wierszu standardowego wejścia znajdują
się dokładnie trzy dodatnie liczby całkowite pooddzielane pojedynczymi
odstępami. Są to odpowiednio: liczby 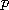 i
i 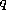 określające parametry
dźwigu oraz liczba
określające parametry
dźwigu oraz liczba  , będąca liczbą początkowych wagonów pociągu
do załadowania. Liczby te spełniają nierówności
, będąca liczbą początkowych wagonów pociągu
do załadowania. Liczby te spełniają nierówności
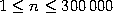 ,
, 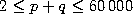 .
.
Wyjście
W pierwszym wierszu standardowego wyjścia powinna znajdować
się dokładnie jedna liczba całkowita 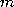 będąca liczbą instrukcji
w wygenerowanym programie.
W każdym z kolejnych
będąca liczbą instrukcji
w wygenerowanym programie.
W każdym z kolejnych 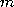 wierszy powinny znajdować się dokładnie
trzy liczby naturalne
wierszy powinny znajdować się dokładnie
trzy liczby naturalne  ,
, 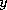 ,
,  pooddzielane pojedynczymi
odstępami,
pooddzielane pojedynczymi
odstępami,
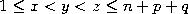 ,
, 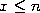 ,
, 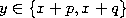 ,
,  .
Są to numery wagonów, na które dźwig ma położyć kontenery
w kolejnym ruchu.
.
Są to numery wagonów, na które dźwig ma położyć kontenery
w kolejnym ruchu.
Przykład
Dla danych wejściowych:
2 3 10
poprawną odpowiedzią jest:
4 1 3 6 2 4 7 5 8 10 9 11 14
Autor zadania: Wojciech Rytter.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English