
Zadanie Mrówka (mro)
Pomóż nam usprawnić bazę zadań!
Mrówka
Limit pamięci: 32 MB
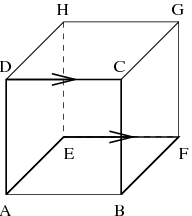
Myśląca bajtocka mrówka chodzi po krawędziach sześcianu ABCDEFGH:
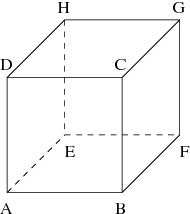
Zastanawia się, na ile sposobów może przejść z zadanego wierzchołka
sześcianu do wskazanego innego, przechodząc dokładnie po 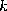 krawędziach
(jeżeli mrówka zaczyna iść po danej krawędzi, to nigdy nie zawróci
i kiedyś dojdzie do drugiego jej końca). Jeżeli mrówka przejdzie
krawędziach
(jeżeli mrówka zaczyna iść po danej krawędzi, to nigdy nie zawróci
i kiedyś dojdzie do drugiego jej końca). Jeżeli mrówka przejdzie
 razy po tej samej krawędzi, to krawędź tą liczymy
razy po tej samej krawędzi, to krawędź tą liczymy  razy.
Mrówka chciałaby, żeby jej trasa była ciekawa, to znaczy, jeżeli w pewnym
momencie mrówka wejdzie po pewnej krawędzi do danego wierzchołka, to
nie chciałaby wyjść z tego wierzchołka w kolejnym kroku po tej samej krawędzi.
razy.
Mrówka chciałaby, żeby jej trasa była ciekawa, to znaczy, jeżeli w pewnym
momencie mrówka wejdzie po pewnej krawędzi do danego wierzchołka, to
nie chciałaby wyjść z tego wierzchołka w kolejnym kroku po tej samej krawędzi.
Ponieważ mrówka potrafi jedynie liczyć od 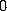 do
do 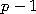 , dla pewnego
, dla pewnego 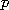 , to podaj jej tylko
resztę z dzielenia przez
, to podaj jej tylko
resztę z dzielenia przez 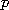 liczby możliwych tras, spełniających
powyższe warunki.
liczby możliwych tras, spełniających
powyższe warunki.
Zadanie
Napisz program który:
-
wczyta ze standardowego wejścia początkowy i końcowy wierzchołek na
trasie mrówki, liczbę krawędzi do pokonania i liczbę
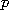 ,
,
-
obliczy resztę z dzielenia przez
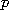 liczby ciekawych tras mrówki
spełniających jej wymagania,
liczby ciekawych tras mrówki
spełniających jej wymagania,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu wejścia znajdują się dwie wielkie litery 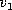 i
i 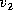 (
(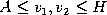 ,
, 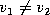 ), oddzielone pojedynczym odstępem i
oznaczające wierzchołki początkowy i końcowy na trasie mrówki.
Drugi wiersz wejścia zawiera dwie liczby całkowite
), oddzielone pojedynczym odstępem i
oznaczające wierzchołki początkowy i końcowy na trasie mrówki.
Drugi wiersz wejścia zawiera dwie liczby całkowite 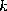 i
i 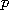 (
(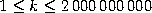 ,
, 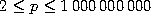 ),
oddzielone pojedynczym odstępem.
),
oddzielone pojedynczym odstępem.
Wyjście
W pierwszym i jedynym wierszu standardowego wyjścia należy zapisać jedną
liczbę całkowitą - resztę z dzielenia przez 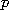 liczby ciekawych tras
mrówki z wierzcholka
liczby ciekawych tras
mrówki z wierzcholka 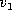 do wierzchołka
do wierzchołka 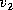 , złożonych z dokładnie
, złożonych z dokładnie 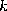 krawędzi sześcianu.
krawędzi sześcianu.
Przykład
Dla danych wejściowych:A B 3 100poprawną odpowiedzią jest:
2
Autor zadania: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English