
Zadanie Gra w zielone (gra)
Pomóż nam usprawnić bazę zadań!
Gra w zielone
Limit pamięci: 32 MB
Gra w zielone jest grą dla dwóch graczy - nazwijmy ich Ania i Bolek - polegającą na przesuwania pionka po planszy.
Część pól planszy jest pokolorowana na zielono, a pozostałe są białe.
Wszystkie pola są ponumerowane
liczbami naturalnymi z zakresu 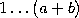 , pola o numerach z zakresu
, pola o numerach z zakresu
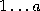 należą do Ani, natomiast pola o numerach
należą do Ani, natomiast pola o numerach  należą do Bolka.
należą do Bolka.
Dla każdego pola dany jest zbiór następników, zawierający te pola planszy, do których można z niego przejść w jednym ruchu. Zbiory te zostały tak dobrane, że z pola należącego do Ani można przejść w jednym ruchu tylko na pole należące do Bolka i odwrotnie.
Na początku gry ustawiamy pionek na dowolnym polu, a następnie gracze na przemian przestawiają pionek ze swojego pola na dowolny następnik tego pola - należący do przeciwnika. Grę rozpoczyna właściciel pola, z którego zaczynamy rozgrywkę. Zakładamy, że wszystkie pola mają niepuste zbiory następników, a więc zawsze można wykonać ruch. Gra kończy się w momencie, gdy pionek stanie po raz drugi na tym samym polu. Jeśli w sekwencji ruchów, od pierwszego do powtórnego zajęcia tego pola, pionek stanął przynajmniej raz na polu zielonym, to wygrywa Ania, w przeciwnym przypadku wygrywa Bolek.
Powiemy, że Ania ma strategię wygrywającą dla danego pola początkowego, jeśli istnieje metoda gwarantująca jej wygraną w rozgrywce zaczynającej się od tego pola, niezależnie od tego, jakie ruchy będzie wykonywał Bolek.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opis planszy do gry w zielone,
- znajdzie zbiór pól planszy, dla których Ania ma strategię wygrywającą,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia zapisane
są dwie nieujemne liczby całkowite  ,
, 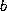 oddzielone
pojedynczym odstępem, oznaczające odpowiednio:
liczbę pól należących do Ani i liczbę pól należących do Bolka.
Liczby
oddzielone
pojedynczym odstępem, oznaczające odpowiednio:
liczbę pól należących do Ani i liczbę pól należących do Bolka.
Liczby  ,
, 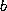 spełniają warunek:
spełniają warunek: 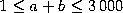 .
W kolejnych a+b wierszach opisano pola planszy - najpierw pola należące
do Ani, a następnie pola należące do Bolka.
Wiersz o numerze
.
W kolejnych a+b wierszach opisano pola planszy - najpierw pola należące
do Ani, a następnie pola należące do Bolka.
Wiersz o numerze 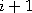 , dla
, dla 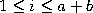 , zawiera na początku
liczby całkowite
, zawiera na początku
liczby całkowite  ,
, 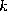 oddzielone pojedynczym odstępem, oznaczające
odpowiednio kolor pola o numerze
oddzielone pojedynczym odstępem, oznaczające
odpowiednio kolor pola o numerze 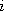 (
(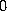 oznacza kolor biały,
oznacza kolor biały,
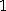 - kolor zielony), oraz liczbę
następników tego pola. Następnie w tym wierszu zapisane jest
- kolor zielony), oraz liczbę
następników tego pola. Następnie w tym wierszu zapisane jest
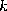 liczb całkowitych (
liczb całkowitych (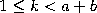 ),
pooddzielanych pojedynczymi odstępami,
będącymi numerami następników danego pola.
Liczba pól zielonych na planszy nie przekracza
),
pooddzielanych pojedynczymi odstępami,
będącymi numerami następników danego pola.
Liczba pól zielonych na planszy nie przekracza 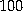 .
Suma liczb następników wszystkich pól na planszy nie przekracza
.
Suma liczb następników wszystkich pól na planszy nie przekracza 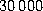 .
.
Wyjście
Pierwszy wiersz standardowego wyjścia powinien zawierać
dokładnie jedną liczbę całkowitą 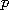 , oznaczającą liczbę pól,
na których Ania ma strategię wygrywającą.
Następne
, oznaczającą liczbę pól,
na których Ania ma strategię wygrywającą.
Następne 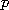 wierszy powinno zawierać numery tych
pól zapisane w kolejności rosnącej - każda liczba powinna
zostać zapisana w osobnym wierszu.
wierszy powinno zawierać numery tych
pól zapisane w kolejności rosnącej - każda liczba powinna
zostać zapisana w osobnym wierszu.
Przykład
Dla danych wejściowych:
5 3 0 2 6 7 0 3 6 7 8 0 1 8 1 1 7 1 1 8 1 2 1 2 0 2 1 2 0 2 3 4
poprawną odpowiedzią jest:
5 1 2 4 6 7
Autor zadania: Marcin Jurdziński.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English