
Zadanie Sznurki (szn)
Pomóż nam usprawnić bazę zadań!
Sznurki
Limit pamięci: 32 MB
Przedsiębiorstwo String-Toys S.A. zwróciło się do Ciebie o pomoc w rozwiązaniu następującego problemu. String-Toys S.A. chce produkować ze sznurka modele spójnych grafów acyklicznych.
Każdy graf składa się z wierzchołków i pewnej liczby krawędzi łączących różne wierzchołki. Ten sam wierzchołek może być połączony z wieloma innymi wierzchołkami. Graf jest spójny i acykliczny, gdy od każdego wierzchołka można przejść do każdego innego wierzchołka wędrując po krawędziach i co więcej, bez zawracania można to zrobić dokładnie na jeden sposób.
Wierzchołki grafów mają być modelowane przez węzły zawiązane na kawałkach sznurka, a krawędzie przez odcinki sznurka pomiędzy węzłami. Każdy węzeł może być wynikiem zasuplenia kawałka sznurka lub związania w tym samym miejscu wielu kawałków. Ze względów technicznych koszty produkcji zależą od liczby kawałków sznurka użytych do wykonania modelu, oraz od długości najdłuższego z kawałków. (Każda krawędź ma długość 1. Długość sznurka użytego do zrobienia węzłów jest pomijalna.)
Zadanie
Zadanie polega na napisaniu programu, który:
- wczyta ze standardowego wejścia opis spójnego grafu acyklicznego, który ma być modelowany,
- obliczy:
- minimalną liczbę kawałków sznurka potrzebnych do wykonania modelu,
- zakładając, że liczba kawałków sznurka jest minimalna, minimalną długość najdłuższego kawałka sznurka potrzebnego do wykonania modelu,
- wypisze dwie obliczone liczby na standardowe wyjście.
Wejście
Pierwszy wiersz zawiera jedną dodatnią liczbę całkowitą  -
liczbę wierzchołków w grafie,
-
liczbę wierzchołków w grafie, 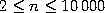 .
Wierzchołki są ponumerowane od 1 do
.
Wierzchołki są ponumerowane od 1 do  .
Kolejne
.
Kolejne 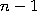 wierszy zawiera opisy krawędzi, po jednej w wierszu.
Każdy z tych wierszy zawiera parę liczb całkowitych
wierszy zawiera opisy krawędzi, po jednej w wierszu.
Każdy z tych wierszy zawiera parę liczb całkowitych  i
i 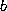 oddzielonych pojedynczym odstępem,
oddzielonych pojedynczym odstępem, 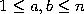 ,
, 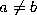 .
Para taka reprezentuje krawędź łączącą wierzchołki
.
Para taka reprezentuje krawędź łączącą wierzchołki  i
i 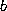 .
.
Wyjście
Twój program powinien wypisać w pierwszym wierszu
wyjścia dwie liczby całkowite 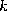 i
i 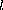 oddzielone pojedynczym
odstępem:
oddzielone pojedynczym
odstępem:
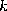 powinno być minimalną liczbą kawałków sznurka potrzebnych do
wykonania modelu grafu, a
powinno być minimalną liczbą kawałków sznurka potrzebnych do
wykonania modelu grafu, a 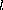 powinno być minimalną długością
najdłuższego kawałka sznurka (zakładając, że zużyliśmy
powinno być minimalną długością
najdłuższego kawałka sznurka (zakładając, że zużyliśmy 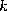 kawałków
sznurka).
kawałków
sznurka).
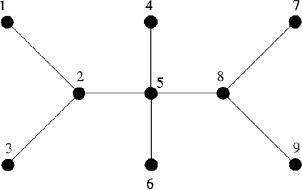
Przykład
Dla danych wejściowych:
9 7 8 4 5 5 6 1 2 3 2 9 8 2 5 5 8
poprawną odpowiedzią jest:
4 2
Autor zadania: Marcin Kubica.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English