
Zadanie Mapka w kratkę (gri)
Pomóż nam usprawnić bazę zadań!
Grid
Memory limit: 32 MB
The map of Byteland is drawn on a grid of size 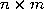 (
( is the vertical dimension,
is the vertical dimension, 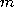 is the horizontal dimension).
The horizontal lines marking the division are called parallels,
and are numbered from
is the horizontal dimension).
The horizontal lines marking the division are called parallels,
and are numbered from 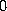 to
to  , while the vertical lines of the division
are called meridians, and are numbered from
, while the vertical lines of the division
are called meridians, and are numbered from 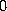 to
to 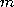 (see figure from the example).
(see figure from the example).
Weather forecasting is a serious issue in Byteland. For each unit square of the grid a certain amount of computation time is required to prepare the forecast. Due to terrain conditions and other factors this time may vary from square to square. Until very recently the forecasting system was processing the unit squares one after another, so it took as long as the sum of all the unit times to prepare the complete forecast.
You have been asked to design a new system, running on a multiprocessor computer.
To share the computations among processors, the area of Byteland
should be divided by  parallels and
parallels and  meridians into
meridians into 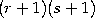 smaller
rectangles.
Each processor will cover one rectangle of this division and will
process the squares of this rectangle one after another.
This way the computation time for such rectangle will be the sum of all
computation times of the unit squares contained in this rectangle.
The computation time of the complete forecast will be the maximum among
computation times of the individual processors.
smaller
rectangles.
Each processor will cover one rectangle of this division and will
process the squares of this rectangle one after another.
This way the computation time for such rectangle will be the sum of all
computation times of the unit squares contained in this rectangle.
The computation time of the complete forecast will be the maximum among
computation times of the individual processors.
Your task is to find the minimal possible computation time for some choice of  parallels and
parallels and  meridians.
meridians.
Task
Write a program, that:
- reads the dimensions of the map of Byteland, the required number of parallels and meridians and the unit computation times from the standard input,
- finds the minimal time required to compute the complete forecast,
- writes the obtained value to the standard output.
Input
The first line of the input contains four integers  ,
, 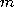 ,
,  and
and  ,
separated by single spaces (
,
separated by single spaces (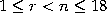 ,
, 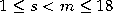 ).
The following
).
The following  lines contain the computation times of the unit squares.
The
lines contain the computation times of the unit squares.
The 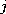 -th number in the
-th number in the 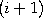 -st line is
-st line is 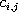 - the time
required to prepare the weather forecast for the unit square located between
the
- the time
required to prepare the weather forecast for the unit square located between
the 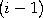 -st and
-st and 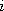 -th parallel and between the
-th parallel and between the 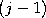 -st and
-st and 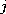 -th
meridian (
-th
meridian (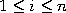 ,
, 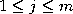 ,
, 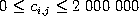 ).
).
Additionally, in test cases worth 40% of points,  and
and 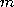 will not exceed
will not exceed 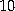 .
.
Output
Your program should write exactly one line. It should contain one integer - the optimal computation time.
Example
For the input data:
7 8 2 1 0 0 2 6 1 1 0 0 1 4 4 4 4 4 3 0 2 4 4 4 4 4 3 0 1 4 4 4 8 4 4 0 0 3 4 4 4 4 4 3 0 1 1 3 4 4 3 0 0 0 0 1 2 1 2 0
the correct result is:
31
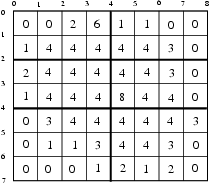
The 2-nd and 4-th parallel and the 4-th meridian divide the country into 6 rectangles with computation times 21, 13, 27, 27, 17, 31. The computation time of the complete forecast is 31.
Task author: Zbigniew Czech.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English