
Zadanie Sieć dróg (sie)
Pomóż nam usprawnić bazę zadań!
Road Net
Memory limit: 32 MB
A diskette was enclosed to a road map.
The diskette contains the table of the shortest ways (distances) between each pair of towns on the map.
All the roads are two-way.
The location of towns on the map has the following interesting property:
if the length of the shortest way from town 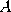 to town
to town 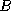 equals the sum of the lengths of
the shortest ways from
equals the sum of the lengths of
the shortest ways from 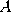 to
to 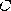 and
and 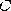 to
to 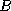 then
town
then
town 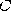 lies on (certain) shortest way from
lies on (certain) shortest way from 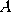 to
to 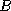 .
We say that towns
.
We say that towns 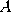 and
and 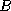 are neighbouring towns if there is no town
are neighbouring towns if there is no town 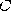 such that
the length of the shortest way from
such that
the length of the shortest way from 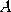 to
to 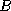 equals the sum of the lengths of
the shortest ways from
equals the sum of the lengths of
the shortest ways from 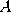 to
to 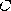 and
and 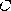 to
to 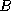 .
.
Find all the pairs of neighbouring towns.
Example
For the table of distances:
A B C A 0 1 2 B 1 0 3 C 2 3 0
the neighbouring towns are 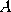 ,
, 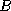 and
and 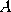 ,
, 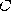 .
.
Task
Write a program that:
- reads the table of distances from the standard input;
- finds all the pairs of neighbouring towns;
- writes the result to the standard output.
Input
In the first line of the standard input there is an integer  ,
, 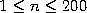 ,
which equals the number of towns on the map.
Towns are numbered from
,
which equals the number of towns on the map.
Towns are numbered from 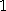 to
to  .
.
The table of distances is written in the following  lines.
In the
lines.
In the 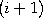 -st line,
-st line, 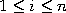 , there are
, there are  non-negative integers not greater than
non-negative integers not greater than 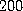 ,
separated by single spaces.
The
,
separated by single spaces.
The 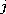 -th integer is the distance between towns
-th integer is the distance between towns 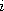 and
and 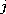 .
.
Output
Your program should write all the pairs of the neighbouring towns (i.e. their numbers) to the standard output.
There should be one pair in each line.
Each pair can appear only once.
The numbers in each pair should be given in increasing order.
Pairs should be ordered so that if the pair 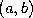 precedes the pair
precedes the pair 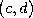 then
then 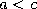 or (
or ( and
and 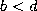 ).
).
Example
For the input data:
3 0 1 2 1 0 3 2 3 0
the correct result is:
1 2 1 3
Task author: Piotr Chrzastowski-Wachtel.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English