
Zadanie Bramki (bra)
Pomóż nam usprawnić bazę zadań!
Gates
Memory limit: 32 MB
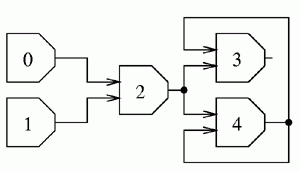
Let us consider a circuit consisting of  gates. The gates are numbered from
gates. The gates are numbered from  to
to 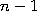 . Each gate has a certain number of inputs and exactly one output. Each of them (inputs and outputs) may be in either one of the states
. Each gate has a certain number of inputs and exactly one output. Each of them (inputs and outputs) may be in either one of the states 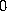 ,
, 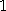 or
or 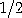 . Each input is connected to exactly one output of some gate. Input's state equals the state of the output it is connected to. Each output may be connected to an arbitrary number of inputs. The gates with numbers
. Each input is connected to exactly one output of some gate. Input's state equals the state of the output it is connected to. Each output may be connected to an arbitrary number of inputs. The gates with numbers  and
and 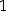 are special - they don't have any input at all while their outputs are always in the following states:
are special - they don't have any input at all while their outputs are always in the following states: 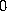 for a gate with a number
for a gate with a number 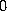 ,
, 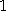 for a gate with a number
for a gate with a number 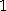 . We say that the state of the output of a gate (in short: gate's state) is valid, if:
. We say that the state of the output of a gate (in short: gate's state) is valid, if:
- it equals
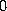 and the gate has more inputs in state
and the gate has more inputs in state 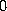 than in state
than in state 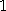 .
. - it equals
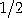 and the gate has the same number of inputs in state
and the gate has the same number of inputs in state 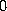 as in state
as in state 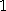 .
. - it equals
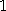 and the gate has more inputs in state
and the gate has more inputs in state 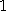 than it has in state
than it has in state 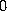 .
. - the gate is special, i.e. it's number is
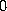 or
or  , and its state is
, and its state is 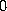 or
or  respectively.
respectively.
We say that a circuit's state is valid if all the states of its gates are valid. We say that a gate's state is fixed if the gate is in the same state in all circuit's valid states.
Task
Write a programme that:
- reads the circuit's description from the standard input,
- for each gate checks if it's state is fixed, and determines it, if so,
- writes the determined states of gates to the standard output.
Input
The first line of the standard input contains the number of gates  ,
, 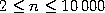 . The following
. The following 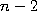 lines contain the descriptions of gates' connections - line no.
lines contain the descriptions of gates' connections - line no. 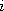 describes inputs of the gate no.
describes inputs of the gate no. 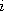 . There is the number
. There is the number 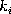 of inputs of this gate, followed by
of inputs of this gate, followed by 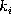 numbers of gates,
numbers of gates,  . Those are the numbers of gates whose outputs are connected to successive inputs of the gate's no.
. Those are the numbers of gates whose outputs are connected to successive inputs of the gate's no. 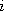 . Numbers in each line are separated by single spaces. The total number of all inputs of all gates does not exceed
. Numbers in each line are separated by single spaces. The total number of all inputs of all gates does not exceed 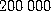 .
.
Output
Your programme should write  lines to the standard output. Depending on the state of gate no.
lines to the standard output. Depending on the state of gate no.  ,
, 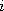 'th line should contain:
'th line should contain:
- 0 - if it is determined and equals
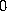 ,
, - 1/2 - if it is determined and equals
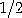 ,
, - 1 - if it is determined and equals
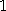 ,
, - ? (question mark) - if it is not determined.
Example
For the input data:
5 2 0 1 2 4 2 2 2 4
the correct result is:
0 1 1/2 ? ?
Task author: Bartosz Walczak.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English