The Competition

Memory limit: 16 MB

At the foot of Mt. Byte there is an entrance to a cave. The cave consists of a complex system of chambers connected with tunnels. The cave entrance leads straight to a chamber called the front chamber. The tunnels do not intersect (they meet only in chambers). Two chambers can either be connected with a single tunnel, or not be connected at all (it may, however, be possible to reach one chamber from the other via remaining chambers). A tunnel always connects two distinct chambers.

It has been decided that 'King's of Byteotia Cup' competition is to be organized. The goal of each competitor is to traverse a freely chosen route in the cave and get out as quickly as possible. The route has to lead through at least one other chamber than the front one. Only two rules are in force: during the travel through the cave each chamber (with the exception of the front chamber) can be visited once at the most, similarly each corridor cannot be crossed more than once.

A famous cave explorer Byteala is preparing himself for the competition. Byteala has been training in the cave for a long time and he has acquired a detailed knowledge of the corridor system. For each corridor he has calculated the amount of time needed to cross it in each direction. The time necessary to move within the chambers can be neglected. Now Byteala would like to calculate a route satisfying requirements of the competition, which can be traversed in the least time possible (the time necessary to traverse a route is the sum of the times needed to cross corridors which it consists of).

Task

Help Byteala! Write a programme which:

• reads from the standard input a description of the cave and times necessary to cross each corridor,
• calculates a route consistent with the requirements, for which the sum of times needed to cross the corridors it comprises is minimal,
• writes to the standard output the time required to traverse the calculated route.

Input

In the first line of the input there are two integers and 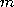(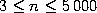, 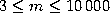) separated by a single space and denoting the number of chambers in the cave and the number of interlinking corridors, respectively. The chambers are numbered from 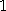to . The front chamber is denoted by 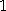. The following 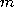lines contain a description of the corridors. In each of these lines there are four integers separated by single spaces. A 4-tuple 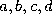means that chambers and 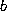are connected with a corridor, the crossing time from to is and from 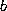to is , , 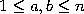, 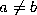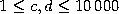. You can assume that a route satisfying requirements of the competition always exists.

Output

Your programme should write in the first (and only) line of the output one integer - the minimal time required to traverse a route satisfying conditions of the competition.

Example

For the input data:

3 3
1 2 4 3
2 3 4 2
1 3 1 1

the correct result is:

6

Task author: Lukasz Kowalik.