Po-łamana

Limit pamięci: 32 MB

W prostokątnym układzie współrzędnych każdy punkt o współrzędnych całkowitych nazywamy p-punktem.

Dowolny odcinek równoległy do jednej z osi współrzędnych, o różnych końcach będących p-punktami, nazywamy p-odcinkiem. Rozważamy odcinki domknięte, tzn. końce należą do odcinka. Łamaną zbudowaną z 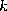p-odcinków, z których każde kolejne dwa są prostopadłe, nazywamy po-łamaną stopnia .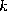

Zadanie

Napisz program, który:

• wczyta ze standardowego wejścia opisy pewnej liczby p-odcinków oraz współrzędne dwóch różnych p-punktów 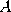i ,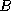
• wyznaczy minimalny stopień po-łamanej łączącej te dwa punkty i nie przecinającej żadnego z danych p-odcinków lub stwierdzi, że taka po-łamana nie istnieje,
• wypisze wynik na standardowe wyjście.

Wejście

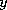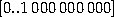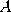Opis p-punktu składa się z dwóch nieujemnych liczb całkowitych oddzielonych pojedynczym odstępem, będących odpowiednio współrzędnymi i tego p-punktu. Liczby te należą do przedziału . W pierwszym wierszu standardowego wejścia znajduje się tylko opis p-punktu . W drugim wierszu znajduje się tylko opis p-punktu 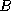. W trzecim wierszu zapisana jest dokładnie jedna nieujemna liczba całkowita będąca liczbą p-odcinków, 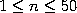. W każdym z kolejnych wierszy znajdują się opisy ydokładnie dwóch p-punktów, oddzielone pojedynczym odstępem. Są to współrzędne końców jednego p-odcinka.

Wyjście

W pierwszym i jedynym wierszu standardowego wyjścia powinna znaleźć się jedna liczba będąca minimalnym stopniem po-łamanej łączącej punkty 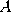i 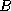oraz nie przecinającej żadnego z zadanych p-odcinków, lub słowo "BRAK", jeśli po-łamana o powyższych własnościach nie istnieje.

Przykład

Dla danych wejściowych:

1 2
3 4
5
0 0 7 0
0 5 7 5
2 2 2 7
4 0 4 3
3 2 6 2

poprawną odpowiedzią jest:

5

Autor zadania: Grzegorz Jakacki.