
Zadanie Wielokąt (wie)
Pomóż nam usprawnić bazę zadań!
Wielokąt
Limit pamięci: 32 MB
Powiemy, że dwa trójkąty przecinają się, jeśli ich wnętrza mają co najmniej jeden wspólny punkt. Wielokąt jest wypukły, jeśli każdy odcinek łączący dowolne dwa punkty tego wielokąta jest w nim zawarty. Trójkątem elementarnym w wielokącie wypukłym nazywamy każdy trójkąt, którego wierzchołki są wierzchołkami tego wielokąta. Triangulacją wielokąta wypukłego nazywamy każdy zbiór elementarnych trójkątów w tym wielokącie, w którym żadne dwa trójkąty nie przecinają się, a wszystkie razem pokrywają cały wielokąt.
Dane są wielokąt i jego triangulacja. Jaka jest największa liczba trójkątów w tej triangulacji, które może przeciąć jeden elementarny trójkąt w tym wielokącie?
Przykład
Rozważmy następującą triangulację:
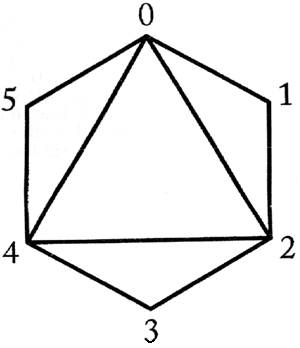
Trójkąt elementarny 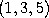 przecina wszystkie trójkąty w tej triangulacji.
przecina wszystkie trójkąty w tej triangulacji.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia liczbę wierzchołków wielokąta i jego triangulację;
- oblicza największą liczbę trójkątów, które przecina pojedynczy elementarny trójkąt w danym wielokącie;
- zapisuje wynik na standardowe wyjście.
Wejście
Pierwszy wiersz standardowego wejścia zawiera liczbę  ,
, 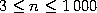 .
Jest to liczba wierzchołków wielokąta.
Wierzchołki wielokąta są ponumerowane kolejno
.
Jest to liczba wierzchołków wielokąta.
Wierzchołki wielokąta są ponumerowane kolejno 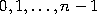 , zgodnie z ruchem wskazówek zegara.
, zgodnie z ruchem wskazówek zegara.
Kolejne 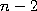 wiersze zawierają opisy trójkątów w triangulacji.
W wierszu
wiersze zawierają opisy trójkątów w triangulacji.
W wierszu 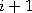 ,
, 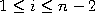 , zapisane są trzy liczby całkowite
, zapisane są trzy liczby całkowite 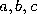 , oddzielone pojedynczymi odstępami.
Są to numery wierzchołków
, oddzielone pojedynczymi odstępami.
Są to numery wierzchołków 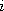 -tego trójkąta w triangulacji.
-tego trójkąta w triangulacji.
Wyjście
W pierwszym i jedynym wierszu standardowego wyjścia należy zapisać jedyną liczbę całkowitą — największą liczbę trójkątów w triangulacji, które przecina jeden elementarny trójkąt w wielokącie wejściowym.
Przykład
Dla danych wejściowych:
6 0 1 2 2 4 3 4 2 0 0 5 4
poprawną odpowiedzią jest:
4
Autor zadania: Krzysztof Diks.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English