Periodicity

Memory limit: 32 MB

Byteasar, the king of Bitotia, has ordained a reform of his subjects' names. The names of Bitotians often contain repeating phrases, e.g., the name Abiabuabiab has two occurrences of the phrase abiab. Byteasar intends to change the names of his subjects to sequences of bits matching the lengths of their original names. Also, he would very much like to reflect the original repetitions in the new names.

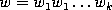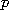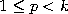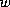In the following, for simplicity, we will identify the upper- and lower-case letters in the names. For any sequence of characters (letters or bits) we say that the integer () is a period of if 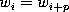for all 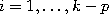. We denote the set of all periods of 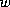by 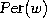. For example, , , 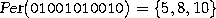and .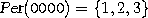

Byteasar has decided that every name is to be changed to a sequence of bits that:

• has length matching that of the original name,
• has the same set of periods as the original name,
• is the smallest (lexicographically¹) sequence of bits satisfying the previous conditions.

Byteasar has asked you to write a program that would facilitate the translation of his subjects' current names into new ones. If you succeed, you may keep your current name as a reward!

Input

In the first line of the standard input there is a single integer 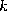- the number of names to be translated (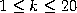). The names are given in the following lines, one in each line. Each name consists of no less than 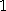and no more than 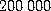upper-case (capital) letters (of the English alphabet).

In the test worth 30% of the points each name consists of at most 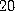letters.

Output

Your program should print 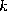lines to the standard output. Each successive line should hold a sequence of zeroes and ones (without spaces in between) corresponding to the names given on the input. If an appropriate sequence of bits does not exists for some names, then "XXX" (without quotation marks) should be printed for that name.

Example

For the input data:

3
ABIABUABIAB
BABBAB
BABURBAB

the correct result is:

01001101001
010010
01000010

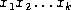¹ The sequence of bits is lexicographically smaller than the sequence of bits 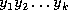if for some 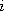, , 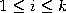we have 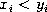and for all 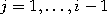we have .

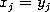Task author: Wojciech Rytter.