
Zadanie Permutacja (per)
Pomóż nam usprawnić bazę zadań!
Permutacja
Limit pamięci: 32 MB
Multizbiorem nazywamy obiekt matematyczny podobny do zbioru,
w którym jednak ten sam element może występować wielokrotnie.
Podobnie jak w przypadku zbioru, także dla multizbioru wszystkie
elementy można ustawić w ciąg i to zazwyczaj na wiele sposobów;
każde takie ustawienie nazywamy permutacją multizbioru.
Dla przykładu, permutacjami multizbioru 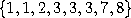 są między innymi
są między innymi 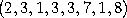 oraz
oraz 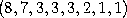 .
.
Powiemy, że jedna permutacja danego multizbioru jest mniejsza (w porządku leksykograficznym) od drugiej, jeżeli na pierwszej pozycji, na której te permutacje się różnią, pierwsza z nich zawiera element mniejszy niż druga. Wszystkie permutacje danego multizbioru można ponumerować (zaczynając od jedynki) w kolejności od najmniejszej do największej.
Zadanie
Napisz program, który:
-
wczyta ze standardowego wejścia opis permutacji pewnego multizbioru
oraz dodatnią liczbę
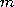 ,
,
-
wyznaczy numer wczytanej permutacji w porządku leksykograficznym,
a dokładniej jego resztę z dzielenia przez
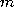 ,
,
- wypisze wynik na standardowe wyjście.
Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite  oraz
oraz 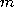 (
(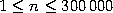 ,
, 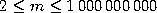 ),
oddzielone pojedynczym odstępem.
Oznaczają one odpowiednio liczbę elementów multizbioru oraz ... liczbę
),
oddzielone pojedynczym odstępem.
Oznaczają one odpowiednio liczbę elementów multizbioru oraz ... liczbę 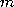 .
Drugi wiersz wejścia zawiera
.
Drugi wiersz wejścia zawiera  dodatnich liczb całkowitych
dodatnich liczb całkowitych 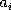 (
(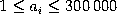 ), pooddzielanych pojedynczymi odstępami
i oznaczających kolejne elementy danej permutacji multizbioru.
), pooddzielanych pojedynczymi odstępami
i oznaczających kolejne elementy danej permutacji multizbioru.
Wyjście
Pierwszy i jedyny wiersz wyjścia powinien zawierać jedną liczbę
całkowitą, oznaczającą resztę z dzielenia przez 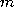 numeru
podanej permutacji w porządku leksykograficznym.
numeru
podanej permutacji w porządku leksykograficznym.
Przykład
Dla danych wejściowych:
4 1000 2 1 10 2
poprawną odpowiedzią jest:
5
Wszystkie permutacje mniejsze od zadanej to (w kolejności leksykograficznej):
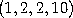 ,
,
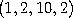 ,
,
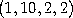 oraz
oraz
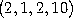 .
.
Autor zadania: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English