
Zadanie Monety (mon)
Pomóż nam usprawnić bazę zadań!
Monety
Limit pamięci: 16 MB
Bajtazar jest niezwykle dumny ze swojej kolekcji rzadkich monet.
Zbierał je przez wiele lat, dbając o to, by żadne dwie nie były do siebie
podobne.
Obecnie ma  monet ponumerowanych tak, że
monet ponumerowanych tak, że 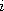 -ta moneta ma rozmiar dokładnie
-ta moneta ma rozmiar dokładnie  .
.
Jako że kolekcja Bajtazara ostatnio się powiększyła, był on zmuszony kupić
nowy klaser.
Jest w nim dokładnie  przegród na monety, każda o określonym rozmiarze.
Oczywiście żadnej monety nie można włożyć do zbyt małej przegrody.
Nic nie stoi jednak na przeszkodzie, by włożyć ją do przegrody większej.
przegród na monety, każda o określonym rozmiarze.
Oczywiście żadnej monety nie można włożyć do zbyt małej przegrody.
Nic nie stoi jednak na przeszkodzie, by włożyć ją do przegrody większej.
Bajtazar zastanawia się teraz do których przegród włożyć poszczególne monety.
Po sprawdzeniu wielu kombinacji zaintrygowało go również pytanie, na ile
sposobów może zapełnić klaser.
Ponieważ liczba ta może być bardzo duża, Bajtazarowi wystarczy jej
reszta z dzielenia przez 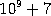 .
Napisz program, który zaspokoi jego ciekawość.
.
Napisz program, który zaspokoi jego ciekawość.
Wejście
Pierwszy wiersz standardowego wejścia zawiera jedną liczbę całkowitą:
 (
(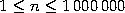 ).
W następnym wierszu znajduje się
).
W następnym wierszu znajduje się  liczb całkowitych
liczb całkowitych 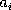 (
( )
pooddzielanych pojedynczymi odstępami. Liczba
)
pooddzielanych pojedynczymi odstępami. Liczba 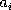 mówi, jaką największą monetę
można włożyć do
mówi, jaką największą monetę
można włożyć do 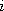 -tej przegrody.
-tej przegrody.
Możesz założyć, że w testach wartych co najmniej  punktów zachodzi dodatkowo
warunek:
punktów zachodzi dodatkowo
warunek: 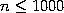 .
.
Wyjście
Twój program powinien wypisać na standardowe wyjście jedną liczbę
całkowitą - resztę z dzielenia liczby sposobów zapełnienia klasera
przez 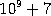 .
.
Przykład
Dla danych wejściowych:
4 4 2 4 2
poprawną odpowiedzią jest:
4
Autor zadania: Michał Włodarczyk.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English