
Zadanie Zdjęcia (zdj)
Pomóż nam usprawnić bazę zadań!
Zdjęcia
Limit pamięci: 32 MB
Mały Bajtek na swoje siódme urodziny dostał od rodziców aparat fotograficzny. Od tego czasu uwielbia robić zdjęcia każdej nowo poznanej osobie. Każde zdjęcie, które zrobi, wywiesza na tablicy korkowej w swoim pokoju. Od urodzin minęło parę miesięcy i tablica jest już mocno zapełniona. Niektóre zdjęcia są całkowicie zasłonięte, inne częściowo... Jeszcze inne, najnowsze, są widoczne w całości.
Kiedy Bajtek przyczepia nowe zdjęcia pinezkami, zastanawia się, ile spośród dotychczas wywieszonych zdjęć przebija każda z nowych pinezek. Chłopiec jest ciekaw, ile zdjęć może maksymalnie przebić jedna taka pinezka. Pomóż Bajtkowi zaspokoić ciekawość.
Zadanie
Napisz program, który
- wczyta ze standardowego wejścia opis zdjęć znajdujących się na tablicy korkowej Bajtka,
- wyznaczy maksymalną liczbę zdjęć, które może przebić pinezka wbita w tablicę,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu wejścia znajduje się jedna liczba całkowita  (
(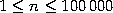 ) - jest to liczba zdjęć na tablicy.
W każdym z następnych
) - jest to liczba zdjęć na tablicy.
W każdym z następnych  wierszy znajdują się po cztery liczby całkowite.
W wierszu
wierszy znajdują się po cztery liczby całkowite.
W wierszu 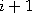 -szym zapisane są liczby
-szym zapisane są liczby 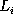 ,
, 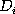 ,
, 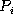 ,
, 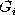 (
(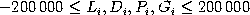 oraz
oraz 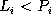 i
i 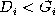 ),
poddzielane pojedynczymi odstępami.
Są to współrzędne zdjęcia w układzie kartezjańskim na tablicy:
),
poddzielane pojedynczymi odstępami.
Są to współrzędne zdjęcia w układzie kartezjańskim na tablicy:
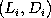 to współrzędne lewego dolnego, natomiast
to współrzędne lewego dolnego, natomiast 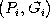 to współrzędne prawego górnego rogu zdjęcia.
Przyjmujemy, że pinezka wbita w punkt
to współrzędne prawego górnego rogu zdjęcia.
Przyjmujemy, że pinezka wbita w punkt 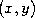 przebije to zdjęcie,
jeśli
przebije to zdjęcie,
jeśli 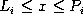 oraz
oraz 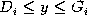 .
.
Wyjście
Twój program powinien wypisać w pierwszym i jedynym wierszu wyjścia jedną liczbę całkowitą - maksymalną liczbę zdjęć, które może przebić pinezka wbita w pewnym miejscu tablicy.
Przykład
Dla danych wejściowych:
5 -1 -1 1 2 0 -2 3 0 2 2 3 3 -1 -1 1 2 2 -1 4 1
poprawną odpowiedzią jest:
3
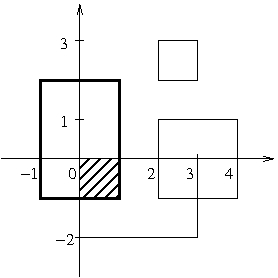
Obszar zakreskowany na rysunku reprezentuje fragment tablicy, w którym należy przyczepić pinezkę, aby przebić 3 zdjęcia. Zauważ, że dwa zdjęcia na tablicy (pierwsze i czwarte) dokładnie się pokrywają.
Autor zadania: Marian M. Kędzierski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English