
Zadanie Szatnia (sza)
Pomóż nam usprawnić bazę zadań!
Szatnia
Limit pamięci: 128 MB
W Bajtocji odbywa się doroczny zlot bogatych mieszkańców. Zbierają się oni, by chwalić się swoimi zarobkami, butami Lebajtina i innymi luksusowymi rzeczami. Naturalnie, nie wszystkie rzeczy wnoszą na bankiet - płaszcze, kurtki czy parasole zostawiają w szatni, by odebrać je, wychodząc.
Na nieszczęście bogaczy szajka bajtockich złodziei planuje włamać
się do szatni i ukraść część pozostawionych tam przedmiotów.
Póki co szef szajki przegląda zaproponowane przez gangsterów plany skoku.
Każdy plan wygląda następująco: złodzieje pojawiają się w szatni w chwili 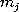 ,
zabierają przedmioty o wartości dokładnie
,
zabierają przedmioty o wartości dokładnie 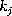 i uciekają, przy czym
cały skok zajmuje im czas
i uciekają, przy czym
cały skok zajmuje im czas 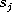 .
Szef gangu chciałby przede wszystkim wiedzieć, które z planów mają szansę
się udać, a które nie.
Plan ma szansę się udać, jeśli w chwili
.
Szef gangu chciałby przede wszystkim wiedzieć, które z planów mają szansę
się udać, a które nie.
Plan ma szansę się udać, jeśli w chwili 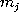 da się uzbierać przedmioty
o łącznej wartości dokładnie
da się uzbierać przedmioty
o łącznej wartości dokładnie 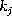 , w taki sposób, żeby do
momentu
, w taki sposób, żeby do
momentu 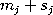 włącznie nikt nie przyszedł po żaden z kradzionych przedmiotów
(w takim wypadku zawiadomiłby ochronę i ucieczka nie udałaby się).
W szczególności, jeśli w chwili
włącznie nikt nie przyszedł po żaden z kradzionych przedmiotów
(w takim wypadku zawiadomiłby ochronę i ucieczka nie udałaby się).
W szczególności, jeśli w chwili 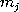 w ogóle nie da się dobrać przedmiotów o łącznej
wartości
w ogóle nie da się dobrać przedmiotów o łącznej
wartości 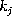 , plan zostaje odrzucony.
Znając moment przyniesienia i zabrania każdego przedmiotu, określ, które
plany mają szansę powodzenia, a które skazane są na porażkę.
Zakładamy, że jeśli przedmiot zostaje przyniesiony w momencie, w którym
złodzieje mają dokonać skoku, mogą go już ukraść (patrz test przykładowy).
, plan zostaje odrzucony.
Znając moment przyniesienia i zabrania każdego przedmiotu, określ, które
plany mają szansę powodzenia, a które skazane są na porażkę.
Zakładamy, że jeśli przedmiot zostaje przyniesiony w momencie, w którym
złodzieje mają dokonać skoku, mogą go już ukraść (patrz test przykładowy).
Wejście
W pierwszym wierszu standardowego wejścia znajduje się liczba całkowita  (
(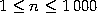 ), reprezentująca liczbę przedmiotów, które zostaną
pozostawione w szatni.
W kolejnych
), reprezentująca liczbę przedmiotów, które zostaną
pozostawione w szatni.
W kolejnych  wierszach znajdują się opisy przedmiotów.
Każdy z nich składa się z trzech liczb całkowitych
wierszach znajdują się opisy przedmiotów.
Każdy z nich składa się z trzech liczb całkowitych 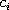 ,
, 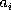 i
i 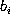 (
(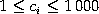 ,
, 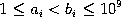 ),
pooddzielanych pojedynczymi odstępami,
oznaczających kolejno: wartość przedmiotu, moment, w którym zostanie
przyniesiony do szatni, oraz moment, w którym zostanie z niej zabrany.
),
pooddzielanych pojedynczymi odstępami,
oznaczających kolejno: wartość przedmiotu, moment, w którym zostanie
przyniesiony do szatni, oraz moment, w którym zostanie z niej zabrany.
Następny wiersz zawiera liczbę 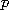 (
(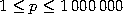 )
- liczbę planów przedstawionych przez szajkę.
Każdy z nich jest opisany w jednym wierszu przez trzy liczby całkowite
)
- liczbę planów przedstawionych przez szajkę.
Każdy z nich jest opisany w jednym wierszu przez trzy liczby całkowite
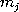 ,
, 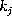 i
i 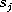 (
(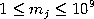 ,
, 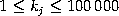 ,
,
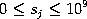 ), pooddzielane pojedynczymi odstępami,
oznaczające kolejno: moment, w którym złodzieje
weszliby do szatni, wartość, jaką chcą uzyskać, oraz czas, jaki zajmie im
kradzież.
), pooddzielane pojedynczymi odstępami,
oznaczające kolejno: moment, w którym złodzieje
weszliby do szatni, wartość, jaką chcą uzyskać, oraz czas, jaki zajmie im
kradzież.
W testach wartych 16% punktów zachodzi dodatkowy warunek
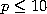 .
.
W innych testach, również wartych 16% punktów, wszystkie
przedmioty mają równe 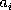 .
.
W jeszcze innych testach, wartych 24% punktów, wszystkie
zapytania mają równe 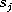 .
.
Wyjście
Dla każdego planu szajki określ, czy plan da się zrealizować, tj. ukraść
przedmioty o wartości dokładnie 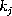 i uciec, zanim ktoś upomni się o swoją
rzecz.
Jeśli plan jest wykonalny, Twój program powinien wypisać na standardowe
wyjście słowo TAK, a w przeciwnym wypadku słowo NIE.
i uciec, zanim ktoś upomni się o swoją
rzecz.
Jeśli plan jest wykonalny, Twój program powinien wypisać na standardowe
wyjście słowo TAK, a w przeciwnym wypadku słowo NIE.
Przykład
Dla danych wejściowych:
5 6 2 7 5 4 9 1 2 4 2 5 8 1 3 9 5 2 7 1 2 7 2 3 2 0 5 7 2 4 1 5
poprawną odpowiedzią jest:
TAK NIE TAK TAK NIE
Autor zadania: Jan Kanty Milczek.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English