Antisymmetry

Memory limit: 32 MB

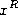Byteasar studies certain strings of zeroes and ones. Let be such a string. By we will denote the reversed (i.e., "read backwards") string , and by we will denote the string obtained from by changing all the zeroes to ones and ones to zeroes.

Byteasar is interested in antisymmetry, while all things symmetric bore him. Antisymmetry however is not a mere lack of symmetry. We will say that a (nonempty) string is antisymmetric if, for every positio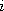n in , the 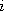-th last character is different than the 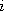-th (first) character. In particular, a string consisting of zeroes and ones is antisymmetric if and only if 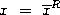. For example, the strings 00001111 and 010101 are antisymmetric, while 1001 is not.

In a given string consisting of zeroes and ones we would like to determine the number of contiguous nonempty antisymmetric fragments. Different fragments corresponding to the same substrings should be counted multiple times.

Input

The first line of the standard input contains an integer (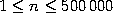) that denotes the length of the string. The second line gives a string of 0 and/or 1 of length . There are no spaces in the string.

Output

The first and only line of the standard output should contain a single integer, namely the number of contiguous (non empty) fragments of the given string that are antisymmetric.

Example

For the input data:

8
11001011

the correct result is:

7

Antisymmetric fragments are: 01 (occurs twice), 10 (also twice), 0101, 1100, and 001011.

Task authors: Jakub Radoszewski, Wojciech Rytter.