
Zadanie Wycieczka (wyc)
Pomóż nam usprawnić bazę zadań!
Excursion
Memory limit: 128 MB
Byteasar is planning a bike trip around Byteland.
He has selected 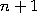 towns that he is going to visit and
towns that he is going to visit and  roads that
connect the pairs of consecutive towns.
Each road can be described using two parameters: its length and
its impression-factor, which could be either positive or negative.
roads that
connect the pairs of consecutive towns.
Each road can be described using two parameters: its length and
its impression-factor, which could be either positive or negative.
The last thing that Byteasar has to do is to divide the trip into
segments that will correspond to consecutive days of the excursion.
Each segment must start and end in one of the selected towns and its length
may not exceed 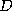 kilometers.
The impression-factor of a segment is defined as a square of the sum of
impression-factors of the roads forming the segment.
More formally, if a segment consists of roads with impression-factors
kilometers.
The impression-factor of a segment is defined as a square of the sum of
impression-factors of the roads forming the segment.
More formally, if a segment consists of roads with impression-factors 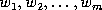 ,
then the impression-factor of the whole segment equals
,
then the impression-factor of the whole segment equals 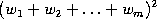 .
.
A bit surprisingly, Byteasar would like to minimize the sum of impression-factors of all the segments in his trip. Even though this idea sounds ridiculous, please help him find out how small sum can he get.
Input
The first line of input contains two integers  and
and 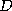 (
(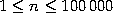 ,
, 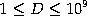 ) that represent the number of roads in
Byteasar's trip and the upper bound for the length of a single segment of the trip.
The following
) that represent the number of roads in
Byteasar's trip and the upper bound for the length of a single segment of the trip.
The following  lines contain descriptions of the roads: the
lines contain descriptions of the roads: the 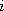 -th line contains two integers
-th line contains two integers
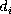 and
and 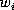 , (
, (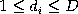 ,
, 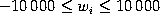 )
that denote the length and the impression-factor of the
)
that denote the length and the impression-factor of the  -th road.
-th road.
Output
The only line of output should contain one integer: the minimum possible sum of impression-factors of all the segments in Byteasar's trip.
Example
For the input data:
5 15 7 4 8 -5 4 2 1 -1 2 4
the correct result is:
14
Task author: Adam Karczmarz.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English