Fibonacci Sums

Memory limit: 32 MB

Fibonacci numbers are an integer sequence defined in the following way: 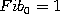, , 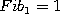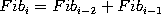(for ). The first few numbers in this sequence are: ().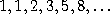

The great computer scientist Byteazar is constructing an unusual computer, in which numbers are represented in Fibonacci system i.e. a bit string 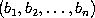denotes the number 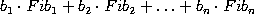. (Note that we do not use 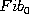.) Unfortunately, such a representation is ambiguous i.e. the same number can have different representations. The number 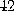, for instance, can be written as: 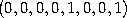, 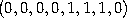or 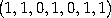. For this very reason, Byteazar has limited himself to only using representations satisfying the following conditions:

• if 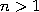, then 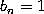, i.e. the representation of a number does not contain leading zeros.
• if 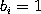, then 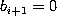(for 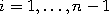), i.e. the representation of a number does not contain two (or more) consecutive ones.

The construction of the computer has proved more demanding than Byteazar supposed. He has difficulties implementing addition. Help him!

Task

Write a programme which:

• reads from the standard input the representations of two positive integers,
• calculates and writes to the standard output the representation of their sum.

Input

The input contains the Fibonacci representations (satisfying the aforementioned conditions) of two positive integers and 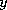- one in the first, the other in the second line. Each of these representations is in the form of a sequence of non-negative integers, separated by single spaces. The first number in the line denotes the length of the representation , 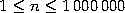. It is followed by zeros and/or ones.

Output

In the first and only line of the output your programme should write the Fibonacci representation (satisfying the aforementioned conditions) of the sum 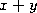. The representation should be in the form of a sequence of non-negative integers, separated by single spaces, as it has been described in the Input section. The first number in the line denotes the length of the representation , 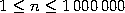. It is followed by zeros and/or ones.

Example

For the input data:

4 0 1 0 1
5 0 1 0 0 1

the correct result is:

6 1 0 1 0 0 1

Task author: Marcin Kubica.