Map 2 [B]

Memory limit: 192 MB

Jane has found an old map of her town in her basement. The map is a square-shaped piece of paper divided into unit squares on which several mysterious points are marked. Jane does not know the meaning of these points and that is why she decided to visit each one of them. She decided to meet with 3 of her colleagues - Jack, Adam and Robert - in one of points for which both map coefficients are integers: this will be the starting point. Afterwards each of the persons will be assigned an area in which he/she will find all the mysterious points and check the secrets hidden in them. Jane decided to settle four areas: the first one that consists of all the points with both coefficients less than the coefficients of the starting point, the second one in which both coefficients are greater, the third one in which the first coefficient is greater and the second one is less, and the fourth one in which the first coefficient is less and the second one is greater. In the end all the colleagues will visit together the marked points for which the first or second coefficient equals the corresponding coefficient of the starting point.

Now Jane only needs to choose the starting point. It should be chosen in such a way that each person will visit independently at least one of the mysterious points. Can you find the number of such starting points?

Input

The first line of the standard input contains two integers and (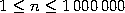, 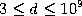), denoting the number of points that are marked on the map and the size of the map. The following lines contain descriptions of the points, each of which has the form of a pair of integers 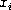, 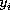(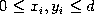), representing the coefficients of the -th point. All points in the input are distinct.

Output

The first and only line of the standard output should contain a single integer representing the number of points that can become the starting point.

Example

For the input data:

6 5
0 0
1 4
2 2
3 2
4 4
5 1

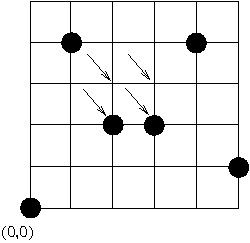
the correct result is:

4

Task author: Jacek Tomasiewicz.