
Zadanie Nawiasy (naw)
Pomóż nam usprawnić bazę zadań!
Nawiasy
Limit pamięci: 32 MB
Działanie odejmowania nie jest łączne, np. 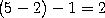 , natomiast
, natomiast 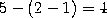 ,
a zatem
,
a zatem 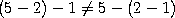 . Wynika stąd, że wartość wyrażenia postaci
. Wynika stąd, że wartość wyrażenia postaci 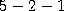 zależy od kolejności wykonywania odejmowań. Zwykle przy braku nawiasów przyjmuje się, że
wykonujemy działania w kolejności od lewej do prawej, czyli wyrażenie
zależy od kolejności wykonywania odejmowań. Zwykle przy braku nawiasów przyjmuje się, że
wykonujemy działania w kolejności od lewej do prawej, czyli wyrażenie 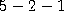 jest równoważne wyrażeniu
jest równoważne wyrażeniu 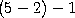 .
.
Mamy dane wyrażenie postaci:
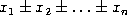
gdzie  oznacza
oznacza  (plus) lub
(plus) lub  (minus), a
(minus), a
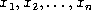 oznaczają (parami) różne zmienne. Chcemy w wyrażeniu postaci:
oznaczają (parami) różne zmienne. Chcemy w wyrażeniu postaci:
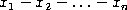
tak rozstawić  par nawiasów, aby jednoznacznie określić kolejność wykonywania
odejmowań i jednocześnie uzyskać wyrażenie równoważne danemu. Na przykład, chcąc uzyskać wyrażenie równoważne wyrażeniu:
par nawiasów, aby jednoznacznie określić kolejność wykonywania
odejmowań i jednocześnie uzyskać wyrażenie równoważne danemu. Na przykład, chcąc uzyskać wyrażenie równoważne wyrażeniu:
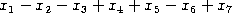
możemy w:
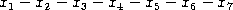
rozmieścić nawiasy w następujący sposób:
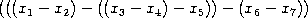 .
.
Uwaga: Interesują nas tylko wyrażenia w pełni i poprawnie ponawiasowane. Wyrażeniem w pełni i poprawnie ponawiasowanym jest
- albo pojedyncza zmienna,
- albo wyrażenie postaci
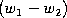 , w którym
, w którym 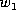 i
i 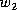 , to
w pełni i poprawnie ponawiasowane wyrażenia.
, to
w pełni i poprawnie ponawiasowane wyrażenia.
 ,
, 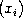 ,
,  lub
lub 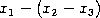 nie jest w pełni ponawiasowane, ponieważ brakuje zewnętrznych nawiasów.
nie jest w pełni ponawiasowane, ponieważ brakuje zewnętrznych nawiasów.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opis danego wyrażenia postaci
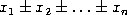 ,
, - obliczy na ile różnych sposobów (modulo
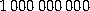 ) można rozstawić
) można rozstawić
 par nawiasów w wyrażeniu
par nawiasów w wyrażeniu 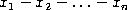 tak, aby
jednoznacznie określić kolejność wykonywania odejmowań i jednocześnie uzyskać wyrażenie równoważne danemu,
tak, aby
jednoznacznie określić kolejność wykonywania odejmowań i jednocześnie uzyskać wyrażenie równoważne danemu, - wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia zapisana jest jedna liczba całkowita  ,
,
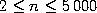 . Jest to liczba zmiennych w danym wyrażeniu. W każdym z kolejnych
. Jest to liczba zmiennych w danym wyrażeniu. W każdym z kolejnych
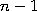 wierszy jest zapisany jeden znak,
wierszy jest zapisany jeden znak,  lub
lub  . W
. W 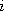 -tym
wierszu zapisany jest znak występujący w danym wyrażeniu między
-tym
wierszu zapisany jest znak występujący w danym wyrażeniu między  a
a 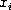 .
.
Wyjście
Twój program powinien zapisać w pierwszym wierszu standardowego wyjścia jedną liczbę całkowitą
równą ilości różnych sposobów (modulo 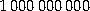 ), na jakie można rozstawić
), na jakie można rozstawić
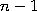 par nawiasów w wyrażeniu
par nawiasów w wyrażeniu 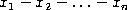 tak, aby jednoznacznie
określić kolejność wykonywania odejmowań i jednocześnie uzyskać wyrażenie równoważne danemu.
tak, aby jednoznacznie
określić kolejność wykonywania odejmowań i jednocześnie uzyskać wyrażenie równoważne danemu.
Przykład
Dla danych wejściowych:
7 - - + + - +
poprawną odpowiedzią jest:
3
Autorzy zadania: Piotr Chrząstowski, Wojciech Guzicki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English