
Zadanie Klocki (klo)
Pomóż nam usprawnić bazę zadań!
Klocki
Limit pamięci: 32 MB
Do przedszkola w Bajtocji chodzi miły chłopczyk Bajtazar. Jego ulubiona zabawa polega na przekładaniu 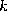 jednakowych klocków
między szufladkami. Jest
jednakowych klocków
między szufladkami. Jest  szufladek ponumerowanych liczbami
szufladek ponumerowanych liczbami 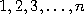 . Dziś przyszła do niego jego ulubiona koleżanka Bajtolina,
żeby oglądać jego zabawę z klockami. Wiadomo, że Bajtolina szybko się nudzi i odchodzi, gdy tylko widzi drugi raz tę samą konfigurację klocków w szufladkach.
Bajtazar chce jak najdłużej utrzymać zainteresowanie koleżanki, musi więc skonstruować jak najdłuższą sekwencję ruchów. W tym celu może wykonywać wyłącznie operacje polegające na wzięciu jednego klocka z dowolnej szufladki i przełożeniu do dowolnej innej.
Wiadomo także, że w ostatnim ruchu Bajtazar musi zostawić klocki w takim samym ułożeniu jak na początku,
bo inaczej przedszkolanka Bajtella każe mu iść do kąta za robienie bałaganu.
. Dziś przyszła do niego jego ulubiona koleżanka Bajtolina,
żeby oglądać jego zabawę z klockami. Wiadomo, że Bajtolina szybko się nudzi i odchodzi, gdy tylko widzi drugi raz tę samą konfigurację klocków w szufladkach.
Bajtazar chce jak najdłużej utrzymać zainteresowanie koleżanki, musi więc skonstruować jak najdłuższą sekwencję ruchów. W tym celu może wykonywać wyłącznie operacje polegające na wzięciu jednego klocka z dowolnej szufladki i przełożeniu do dowolnej innej.
Wiadomo także, że w ostatnim ruchu Bajtazar musi zostawić klocki w takim samym ułożeniu jak na początku,
bo inaczej przedszkolanka Bajtella każe mu iść do kąta za robienie bałaganu.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia liczby
 i
i 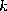 ,
,
- wyznaczy najdłuższą możliwą sekwencję kolejnych stanów ułożenia klocków w szufladkach,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu znajdują się dwie liczby całkowite  oraz
oraz 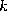 (
(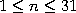 ,
, 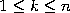 ).
).
Wyjście
Powinno zawierać po jednym napisie w kolejnych wierszach oznaczających kolejne ułożenie klocków w szufladkach.
Każdy taki napis musi się składać z dokładnie  cyfr ze zbioru
cyfr ze zbioru 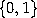 , z czego dokładnie
, z czego dokładnie 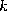 to cyfry
to cyfry 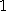 .
Jeśli na
.
Jeśli na 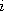 -tej pozycji tego napisu jest cyfra
-tej pozycji tego napisu jest cyfra 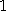 oznacza to klocek w
oznacza to klocek w 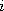 -tej szufladce.
Cyfra
-tej szufladce.
Cyfra 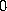 na
na 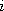 -tej pozycji oznacza odpowiednio brak klocka w
-tej pozycji oznacza odpowiednio brak klocka w 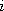 -tej szufladce.
Pierwszy i ostatni wiersz muszą zawierać po takim samym napisie mającym
-tej szufladce.
Pierwszy i ostatni wiersz muszą zawierać po takim samym napisie mającym 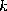 jedynek na początku oraz
jedynek na początku oraz 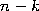 zer.
Oprócz tych wierszy nie może istnieć inna powtarzająca się para.
Dwa kolejne wiersze mogą się różnić pozycją co najwyżej jednej jedynki.
Dowolna najdłuższa sekwencja spełniająca powyższe warunki będzie akceptowana jako poprawna odpowiedź.
Dane dobrane są tak, że wyjście będzie miało co najwyżej
zer.
Oprócz tych wierszy nie może istnieć inna powtarzająca się para.
Dwa kolejne wiersze mogą się różnić pozycją co najwyżej jednej jedynki.
Dowolna najdłuższa sekwencja spełniająca powyższe warunki będzie akceptowana jako poprawna odpowiedź.
Dane dobrane są tak, że wyjście będzie miało co najwyżej 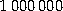 linii.
linii.
Przykład
Dla danych wejściowych:
4 2
poprawną odpowiedzią jest:
1100 1010 1001 0011 0101 0110 1100
Autor zadania: Jakub Pawlewicz.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English