
Zadanie Klub Prawoskrętnych Kierowców (kpk)
Pomóż nam usprawnić bazę zadań!
The Right-Turn Drivers' Club
Memory limit: 32 MB
We are given a rectangular city map comprising 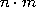 squares
(
squares
(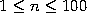 and
and 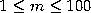 ). The rows of
squares of the map are numbered successively from top to bottom by numbers from
). The rows of
squares of the map are numbered successively from top to bottom by numbers from
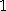 to
to  , and the columns from left to right successively
from
, and the columns from left to right successively
from 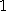 to
to 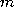 . Each square is either free or blocked.
Vehicular traffic is allowed only on free squares. From each free square one may
move to a free square adjacent to it (i.e. a square that shares a side with it),
however one is not allowed to turn back, i.e. to go back to a square
. Each square is either free or blocked.
Vehicular traffic is allowed only on free squares. From each free square one may
move to a free square adjacent to it (i.e. a square that shares a side with it),
however one is not allowed to turn back, i.e. to go back to a square
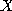 immediately after moving from
immediately after moving from 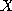 to an adjacent square
to an adjacent square
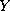 .
.
The Right-Turn Drivers' Club ordered a computer program, which for any two
different squares 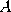 and
and 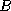 decides whether it is possible
to drive from
decides whether it is possible
to drive from 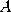 to
to 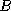 without turning left, and if so, the
program finds such a route with the minimal length. The length of a route is the
number of all its squares. The squares
without turning left, and if so, the
program finds such a route with the minimal length. The length of a route is the
number of all its squares. The squares 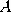 and
and 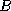 are also
considered squares of the route from
are also
considered squares of the route from 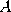 to
to 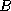 .
.
Task
Write a program that:
- reads from the standard input data on a rectangular network of squares
(i.e. the number of rows
 , the number of columns
, the number of columns 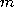 and
the state of each square), and next the coordinates of two different squares
and
the state of each square), and next the coordinates of two different squares
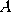 and
and 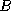 ;
; - decides whether there exists a route without left turns from
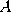 to
to 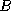 .
If not, the program writes one word NIE ("no") in the standard
output.
If so, the program finds one of the shortest routes without left turns and
writes it in the standard output.
If at least one of the squares
.
If not, the program writes one word NIE ("no") in the standard
output.
If so, the program finds one of the shortest routes without left turns and
writes it in the standard output.
If at least one of the squares 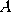 ,
, 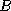 is not free, then the
answer is NIE.
is not free, then the
answer is NIE.
Input
In the first line of the standard input there are two integers separated by a
single space: the number of rows  and the number of columns
and the number of columns
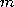 . In each of the following
. In each of the following  lines of the file there is a
description of the corresponding row of the map. Such a description has a form
of one word of length
lines of the file there is a
description of the corresponding row of the map. Such a description has a form
of one word of length 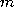 consisting of digits
consisting of digits 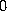 and
and
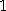 . The digit
. The digit 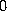 means that the corresponding square is
free, and the digit
means that the corresponding square is
free, and the digit 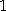 that it is blocked.
that it is blocked.
Next, in one line, there are two coordinates of the square 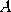 ,
separated by a single space: the row number not greater than
,
separated by a single space: the row number not greater than  and
the column number not greater than
and
the column number not greater than 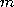 . In the following line there are
two coordinates of the square
. In the following line there are
two coordinates of the square 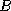 , written the same way.
, written the same way.
The data in the standard input are written correctly and your program need not verify that.
Output
The following should be written in the standard output:
- either one word NIE, if there exist no route without left turns
from
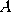 to
to 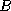 or at least one of the squares
or at least one of the squares 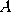 ,
,
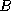 is blocked.
is blocked. - or a description of one of the routes with no left turns from
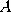 to
to 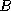 having the minimal length; in that case one should write the
length of the route
having the minimal length; in that case one should write the
length of the route  in the first line, and in each of the following
in the first line, and in each of the following
 lines - two coordinates of the successive square of the route,
separated by a single space.
lines - two coordinates of the successive square of the route,
separated by a single space.
Examples
For the input data:
8 9 010011101 011010101 000000000 111010101 101000100 111010101 000000000 101011111 2 6 1 3
the correct result is:
NIE
For the input data:
8 9 010011101 011010101 000000000 111010101 101000100 111010101 000000000 101011111 2 6 3 8
the correct result is:
12 2 6 3 6 4 6 5 6 5 5 5 4 4 4 3 4 3 5 3 6 3 7 3 8
Task author: Piotr Chrzastowski-Wachtel.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English