
Zadanie Wyspa (wys)
Pomóż nam usprawnić bazę zadań!
Wyspa
Limit pamięci: 32 MB
Na wyspie o kształcie wielokąta wypukłego o 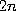 bokach, znajduje się
bokach, znajduje się
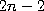 państw - trójkątów, których wierzchołki są
jednocześnie wierzchołkami wielokąta.
Nie ma państw graniczących dokładnie z dwoma
innymi państwami (zatem każde państwo graniczy albo tylko z jednym
państwem, albo z trzema).
państw - trójkątów, których wierzchołki są
jednocześnie wierzchołkami wielokąta.
Nie ma państw graniczących dokładnie z dwoma
innymi państwami (zatem każde państwo graniczy albo tylko z jednym
państwem, albo z trzema).
Wynika stąd, że istnieje dokładnie  państw graniczących tylko z
jednym państwem (są to państwa nadmorskie) oraz
państw graniczących tylko z
jednym państwem (są to państwa nadmorskie) oraz
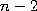 państw graniczących z trzema sąsiadami
(są to państwa wewnątrzlądowe).
Państwa nadmorskie są ponumerowane liczbami od
państw graniczących z trzema sąsiadami
(są to państwa wewnątrzlądowe).
Państwa nadmorskie są ponumerowane liczbami od 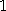 do
do  ,
natomiast państwa wewnątrzlądowe mają numery od
,
natomiast państwa wewnątrzlądowe mają numery od 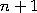 do
do 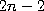 .
.
Gdy podróżujemy z jednego państwa do drugiego, to za przekroczenie każdej granicy musimy zapłacić ustaloną stawkę. Poszczególne stawki mogą być różne, ale przekroczenie granicy w obu kierunkach kosztuje tyle samo.
Dla każdych dwóch państw, spośród  państw nadmorskich, znana jest
suma opłat granicznych na drodze prowadzącej (lądem)
od jednego państwa do drugiego
przez najmniejszą liczbę granic.
Zadanie polega na wyznaczeniu wszystkich opłat granicznych na całej wyspie.
Dla każdego państwa nadmorskiego należy podać numer państwa, z
którym ono graniczy, oraz wysokość odpowiedniej opłaty granicznej.
Ponadto, dla każdego z
państw nadmorskich, znana jest
suma opłat granicznych na drodze prowadzącej (lądem)
od jednego państwa do drugiego
przez najmniejszą liczbę granic.
Zadanie polega na wyznaczeniu wszystkich opłat granicznych na całej wyspie.
Dla każdego państwa nadmorskiego należy podać numer państwa, z
którym ono graniczy, oraz wysokość odpowiedniej opłaty granicznej.
Ponadto, dla każdego z  państw wewnątrzlądowych
należy podać numery trzech państw, z którymi ono graniczy, oraz wysokości
opłat na granicach z tymi państwami.
państw wewnątrzlądowych
należy podać numery trzech państw, z którymi ono graniczy, oraz wysokości
opłat na granicach z tymi państwami.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia sumy opłat granicznych na drogach pomiędzy poszczególnymi państwami nadmorskimi,
- obliczy opłaty graniczne na całej wyspie i wyznaczy, które państwa sąsiadują z którymi,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia
znajduje się jedna dodatnia liczba całkowita  ,
,
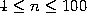 . Jest to liczba państw nadmorskich.
W każdym z następnych
. Jest to liczba państw nadmorskich.
W każdym z następnych  wierszy znajduje się
wierszy znajduje się  nieujemnych liczb
całkowitych oddzielonych pojedynczymi odstępami.
Liczba
nieujemnych liczb
całkowitych oddzielonych pojedynczymi odstępami.
Liczba 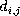 , stojąca na
, stojąca na 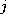 -tym miejscu w
-tym miejscu w 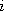 -tym z tych wierszy,
jest równa sumie opłat granicznych na drodze prowadzącej
(lądem, przez najmniejszą liczbę granic) z państwa
o numerze
-tym z tych wierszy,
jest równa sumie opłat granicznych na drodze prowadzącej
(lądem, przez najmniejszą liczbę granic) z państwa
o numerze 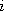 do państwa o numerze
do państwa o numerze 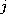 .
Zakładamy przy tym, że na każdej granicy opłata graniczna jest liczbą
całkowitą z przedziału
.
Zakładamy przy tym, że na każdej granicy opłata graniczna jest liczbą
całkowitą z przedziału 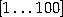 .
Oczywiście,
.
Oczywiście, 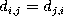 oraz
oraz 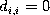 .
.
Wyjście
W pierwszych  wierszach standardowego wyjścia należy zapisać
po dwie liczby całkowite oddzielone pojedynczym ostępem.
Pierwszą liczbą w
wierszach standardowego wyjścia należy zapisać
po dwie liczby całkowite oddzielone pojedynczym ostępem.
Pierwszą liczbą w 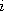 -tym wierszu powinien być numer państwa graniczącego
z państwem o numerze
-tym wierszu powinien być numer państwa graniczącego
z państwem o numerze 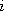 , a drugą wysokość opłaty granicznej na
granicy między tymi dwoma państwami.
W każdym z następnych
, a drugą wysokość opłaty granicznej na
granicy między tymi dwoma państwami.
W każdym z następnych 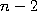 wierszy należy zapisać po
sześć liczb oddzielonych pojedynczymi odstępami.
W wierszu o numerze
wierszy należy zapisać po
sześć liczb oddzielonych pojedynczymi odstępami.
W wierszu o numerze 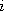 (licząc od początku pliku, a więc
(licząc od początku pliku, a więc 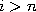 )
pierwszą liczbą ma być numer pierwszego państwa graniczącego
z państwem o numerze
)
pierwszą liczbą ma być numer pierwszego państwa graniczącego
z państwem o numerze 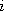 ,
drugą ma być wysokość opłaty granicznej na tej granicy,
trzecią ma być numer drugiego państwa graniczącego z
państwem o numerze
,
drugą ma być wysokość opłaty granicznej na tej granicy,
trzecią ma być numer drugiego państwa graniczącego z
państwem o numerze 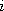 ,
czwartą wysokość opłaty granicznej na drugiej granicy,
piątą ma być numer trzeciego państwa graniczącego z
państwem o numerze
,
czwartą wysokość opłaty granicznej na drugiej granicy,
piątą ma być numer trzeciego państwa graniczącego z
państwem o numerze 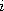 ,
szóstą ma być wysokość opłaty granicznej na trzeciej granicy.
Państwa wewnątrzlądowe mogą być ponumerowane dowolnie liczbami
od
,
szóstą ma być wysokość opłaty granicznej na trzeciej granicy.
Państwa wewnątrzlądowe mogą być ponumerowane dowolnie liczbami
od 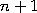 do
do 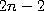 .
.
Przykład
Dla danych wejściowych:
7 0 8 10 8 13 11 14 8 0 8 10 11 5 12 10 8 0 12 5 11 6 8 10 12 0 15 13 16 13 11 5 15 0 14 3 11 5 11 13 14 0 15 14 12 6 16 3 15 0
poprawną odpowiedzią jest:
12 3 10 1 9 1 12 5 8 1 10 4 8 2 5 1 7 2 9 3 3 1 8 3 11 4 2 1 6 4 11 2 9 4 10 2 12 2 1 3 4 5 11 2
![[ rysunek do przykładu ]](images/OI8/wyspa.gif)
Autor zadania: Wojciech Guzicki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English