
Zadanie Korale (kor)
Pomóż nam usprawnić bazę zadań!
Korale
Limit pamięci: 64 MB
Bajtazar postanowił zająć się produkcją naszyjników.
Udało mu się okazyjnie kupić bardzo długi sznur różnokolorowych korali.
Dysponuje on maszyną, która dla zadanego 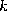 (
(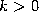 ) potrafi pociąć sznur
na odcinki składające się z
) potrafi pociąć sznur
na odcinki składające się z 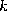 korali (czyli pierwszy odcinek składa
się z korali o numerach
korali (czyli pierwszy odcinek składa
się z korali o numerach 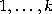 , drugi
, drugi 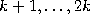 , itd.).
Jeśli sznur korali ma długość, która nie jest wielokrotnością
, itd.).
Jeśli sznur korali ma długość, która nie jest wielokrotnością 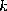 , to
ostatni odcinek, który ma długość mniejszą niż
, to
ostatni odcinek, który ma długość mniejszą niż 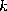 , jako
niepełnowartościowy, nie jest wykorzystywany.
Kolory korali oznaczamy dalej dodatnimi liczbami całkowitymi.
, jako
niepełnowartościowy, nie jest wykorzystywany.
Kolory korali oznaczamy dalej dodatnimi liczbami całkowitymi.
Bajtazar lubi różnorodność i zastanawia się, jak dobrać liczbę 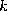 ,
tak by otrzymać jak najwięcej różnych sznurów korali.
Sznur korali, który ma zostać pocięty, ma wyraźnie określony koniec,
od którego zaczynamy odcinać krótsze sznury.
Jednak każdy odcięty sznur może zostać obrócony - inaczej mówiąc,
sznury
,
tak by otrzymać jak najwięcej różnych sznurów korali.
Sznur korali, który ma zostać pocięty, ma wyraźnie określony koniec,
od którego zaczynamy odcinać krótsze sznury.
Jednak każdy odcięty sznur może zostać obrócony - inaczej mówiąc,
sznury 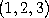 i
i 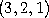 są dla Bajtazara takie same.
Napisz program, który pomoże mu wyznaczyć optymalną wartość parametru
są dla Bajtazara takie same.
Napisz program, który pomoże mu wyznaczyć optymalną wartość parametru 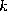 .
.
Przykładowo, dla sznura korali postaci:
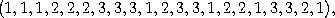
-
stosując
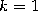 , możemy otrzymać 3 różne sznury korali:
, możemy otrzymać 3 różne sznury korali:
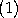 ,
, 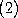 ,
, 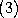 ,
,
-
stosując
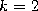 , możemy otrzymać 6 różnych sznurów korali:
, możemy otrzymać 6 różnych sznurów korali:
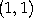 ,
, 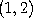 ,
, 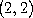 ,
, 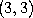 ,
, 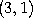 ,
, 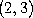 ,
,
-
stosując
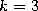 , możemy otrzymać 5 różnych sznurów korali:
, możemy otrzymać 5 różnych sznurów korali:
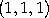 ,
, 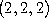 ,
, 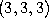 ,
, 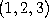 ,
, 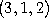 ,
,
-
stosując
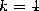 , możemy otrzymać 5 różnych sznurów korali:
, możemy otrzymać 5 różnych sznurów korali:
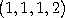 ,
, 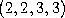 ,
, 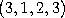 ,
, 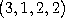 ,
, 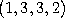 ,
,
-
dla większych wartości
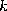 możemy uzyskać co najwyżej 3 różne sznury korali.
możemy uzyskać co najwyżej 3 różne sznury korali.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się liczba całkowita  (
(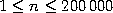 ), oznaczająca długość sznura korali.
W drugim wierszu znajduje się
), oznaczająca długość sznura korali.
W drugim wierszu znajduje się  dodatnich liczb całkowitych
dodatnich liczb całkowitych 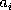 (
(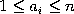 ), pooddzielanych pojedynczymi odstępami i oznaczających
kolory kolejnych korali w sznurze Bajtazara.
), pooddzielanych pojedynczymi odstępami i oznaczających
kolory kolejnych korali w sznurze Bajtazara.
Wyjście
W pierwszym wierszu standardowego wyjścia należy wypisać dwie liczby
całkowite oddzielone pojedynczym odstępem: liczbę różnych sznurów korali,
które można uzyskać przy optymalnym wyborze parametru 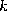 , oraz liczbę
, oraz liczbę 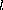 różnych wyborów parametru
różnych wyborów parametru 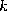 prowadzących do uzyskania takiej liczby sznurów.
Drugi wiersz powinien zawierać
prowadzących do uzyskania takiej liczby sznurów.
Drugi wiersz powinien zawierać 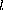 liczb pooddzielanych pojedynczymi odstępami:
wartości parametru
liczb pooddzielanych pojedynczymi odstępami:
wartości parametru 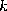 , dla których uzyskujemy optymalne rozwiązanie
- mogą one zostać wypisane w dowolnej kolejności.
, dla których uzyskujemy optymalne rozwiązanie
- mogą one zostać wypisane w dowolnej kolejności.
Przykład
Dla danych wejściowych:
21 1 1 1 2 2 2 3 3 3 1 2 3 3 1 2 2 1 3 3 2 1
poprawną odpowiedzią jest:
6 1 2
Autor zadania: Tomasz Waleń.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English