
Zadanie okn (okn)
Pomóż nam usprawnić bazę zadań!
Okno
Limit pamięci: 32 MB
W prostokątnym układzie współrzędnych dany jest wielokąt o bokach równoległych do osi układu. Każde dwa kolejne boki w tym wielokącie są do siebie prostopadłe, a każdy wierzchołek ma współrzędne całkowitoliczbowe. Dane jest również okno, czyli prostokąt o bokach równoległych do osi układu. Wnętrze wielokąta (ale nie jego brzeg) zostało pokolorowane na czerwono. Jaka jest liczba rozłącznych czerwonych fragmentów wielokąta widzianych przez okno?
Przykład
Przyjrzyjmy się rysunkowi poniżej:
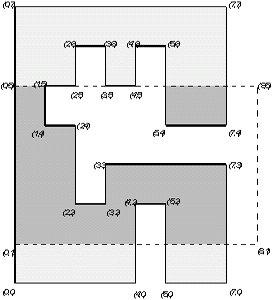
Liczba parami rozłącznych fragmentów wielokąta widzianych przez okno wynosi 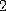 .
.
Zadanie
Napisz program, który:
- wczytuje opisy okna i wielokąta ze standardowego wejścia;
- oblicza liczbę parami rozłącznych czerwonych fragmentów wielokąta widzianych przez okno;
- zapisuje wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia znajdują się cztery liczby całkowite 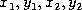 z przedziału
z przedziału 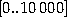 oddzielone pojedynczymi odstępami.
Liczby
oddzielone pojedynczymi odstępami.
Liczby 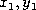 są współrzędnymi górnego lewego rogu okna.
Liczby
są współrzędnymi górnego lewego rogu okna.
Liczby 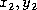 są współrzędnymi dolnego prawego rogu okna.
są współrzędnymi dolnego prawego rogu okna.
Następny wiersz pliku wejściowego zawiera liczbę całkowitą  ,
, 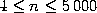 .
Jest to liczba wierzchołków wielokąta.
W kolejnych
.
Jest to liczba wierzchołków wielokąta.
W kolejnych  wierszach znajdują się współrzędne kolejnych wierzchołków wielokąta danych w kierunku przeciwnym do ruchu wskazówek zegara,
tzn. wnętrze wielokąta leży po lewej stronie jego brzegu, gdy przesuwamy się wzdłuż boków wielokąta zgodnie z zadanym porządkiem.
Każdy wiersz zawiera dwie liczby całkowite
wierszach znajdują się współrzędne kolejnych wierzchołków wielokąta danych w kierunku przeciwnym do ruchu wskazówek zegara,
tzn. wnętrze wielokąta leży po lewej stronie jego brzegu, gdy przesuwamy się wzdłuż boków wielokąta zgodnie z zadanym porządkiem.
Każdy wiersz zawiera dwie liczby całkowite 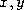 oddzielone pojedynczym odstępem,
oddzielone pojedynczym odstępem, 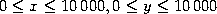 .
Liczby w wierszu
.
Liczby w wierszu 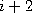 ,
, 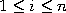 , są współrzędnymi
, są współrzędnymi 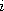 -tego wierzchołka wielokąta.
-tego wierzchołka wielokąta.
Wyjście
Twój program powinien zapisać w pierwszym i jedynym wierszu standardowego wyjścia jedną liczbę całkowitą, a mianowicie — liczbę rozłącznych czerwonych fragmentów wielokąta widzianych przez okno.
Przykład
Dla danych wejściowych:
0 5 8 1 24 0 0 4 0 4 2 5 2 5 0 7 0 7 3 3 3 3 2 2 2 2 4 1 4 1 5 2 5 2 6 3 6 3 5 4 5 4 6 5 6 5 4 7 4 7 7 0 7
poprawną odpowiedzią jest:
2
Autor zadania: Wojciech Guzicki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English