
Zadanie Nawiasy [B] (naw)
Pomóż nam usprawnić bazę zadań!
Nawiasy [B]
Limit pamięci: 64 MB
Poprawnym nawiasowaniem nazywamy taki napis, złożony z nawiasów okrągłych ( i ), w którym jest tyle samo nawiasów otwierających co zamykających oraz każdy prefiks zawiera co najmniej tyle nawiasów otwierających co zamykających. Tak więc ()() jest poprawnym nawiasowaniem, lecz ())( nie, gdyż prefiks ()) zwiera więcej nawiasów zamykających niż otwierających.
Spośród dwóch różnych nawiasowań o długości  powiemy, że wcześniejsze jest to,
które ma nawias otwierający na pierwszej pozycji, na której nawiasowania te się różnią.
Takie uporządkowanie jest równoznaczne z porządkiem leksykograficznym,
przy założeniu, że
powiemy, że wcześniejsze jest to,
które ma nawias otwierający na pierwszej pozycji, na której nawiasowania te się różnią.
Takie uporządkowanie jest równoznaczne z porządkiem leksykograficznym,
przy założeniu, że 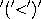 .
.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia liczby
 oraz
oraz 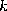 ,
,
- znajdzie
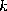 -te w kolejności nawiasowanie spośród wszystkich poprawnych nawiasowań długości
-te w kolejności nawiasowanie spośród wszystkich poprawnych nawiasowań długości 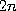 (nawiasowania numerujemy od jedynki),
(nawiasowania numerujemy od jedynki),
- wypisze wynik na standardowe wyjście.
Wejście
Wejście zawiera dokładnie dwie liczby naturalne  oraz
oraz 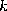 (
(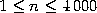 ,
, 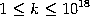 ), oddzielone pojedynczym odstępem.
), oddzielone pojedynczym odstępem.
Wyjście
W pierwszym i jedynym wierszu wyjścia powinno znaleźć się 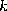 -te w kolejności
nawiasowanie spośród wszystkich poprawnych nawiasowań o długości
-te w kolejności
nawiasowanie spośród wszystkich poprawnych nawiasowań o długości 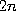 .
Dane testowe są tak dobrane, że żądane nawiasowanie zawsze istnieje.
.
Dane testowe są tak dobrane, że żądane nawiasowanie zawsze istnieje.
Przykład
Dla danych wejściowych:3 2poprawną odpowiedzią jest:
(()())
Autor zadania: Krzysztof Dulęba.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English