Euler's Problem

Memory limit: 128 MB

In this problem we recall the great mathematician Leonhard Euler (1707-1783) and investigate his well-known totient function, .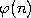

The value of 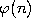for positive integer is the number of integers 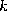(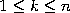) that are coprime with . Two integers are called coprime if their only common positive divisor is 1. For example, we have 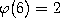, since 1 and 5 are coprime with 6, whereas 2, 3, 4 and 6 are not.

A problem that could have been stated by Euler is as follows: given a positive integer , find all positive integers that satisfy the equation:

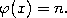
Input

The first line of input contains one integer 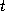(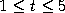) that denotes the number of test cases. 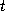lines follow with descriptions of respective test cases. Each such description consists of a single integer ().

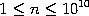Output

Your program should output the answers to the respective test cases. For each test case it should write two lines. The first line should contain the number of solutions of the equation. The second line should contain all solutions listed in increasing order. If the equation does not have any solution, for the corresponding test case your program should write an empty second line.

Example

For the input data:

4
8
10
13
6

the correct result is:

5
15 16 20 24 30
2
11 22
0

4
7 9 14 18