
Zadanie Gonitwa (gon)
Pomóż nam usprawnić bazę zadań!
Chase
Memory limit: 32 MB
Chase is a two-person board game, we call the players 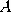 and
and 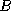 .
A board consists of squares numbered from
.
A board consists of squares numbered from 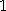 to
to  .
For each pair of different squares it is known if they are adjacent to one another or they are not.
Each player has a piece at his disposal.
At the beginning of a game pieces of players are placed on fixed, distinct squares.
In one turn a player can leave his piece on the square it stands or move it to an adjacent square.
.
For each pair of different squares it is known if they are adjacent to one another or they are not.
Each player has a piece at his disposal.
At the beginning of a game pieces of players are placed on fixed, distinct squares.
In one turn a player can leave his piece on the square it stands or move it to an adjacent square.
A game board has the following properties:
- it contains no triangles, i.e. there are no three distinct squares such that each pair of them is adjacent,
- each square can be reached by each player.
A game consists of many turns.
In one turn each player makes a single move.
Each turn is started by player 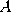 .
.
We say that player 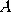 is caught by player
is caught by player 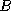 if both pieces stand on the same square.
Decide, if for a given initial positions of pieces, player
if both pieces stand on the same square.
Decide, if for a given initial positions of pieces, player 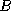 can catch player
can catch player 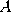 ,
independently of the moves of his opponent.
If so, how many turns player
,
independently of the moves of his opponent.
If so, how many turns player 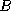 needs to catch player
needs to catch player 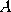 if both play optimally
(i.e. player
if both play optimally
(i.e. player 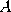 tries to run away as long as he can and player
tries to run away as long as he can and player 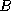 tries to catch him as quickly as possible).
tries to catch him as quickly as possible).
Example
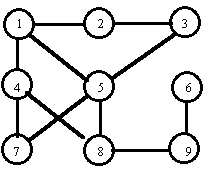
Consider the board in the figure.
Adjacent squares (denoted by circles) are connected by edges.
If at the beginning of a game pieces of players 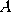 and
and 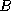 stand on the squares
stand on the squares 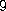 and
and  respectively,
then player
respectively,
then player 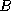 can catch player
can catch player 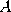 in the third turn (if both players move optimally).
If game starts with pieces on the squares
in the third turn (if both players move optimally).
If game starts with pieces on the squares 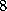 (player
(player 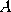 ) and
) and  (player
(player 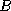 ) then player
) then player 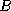 cannot catch player
cannot catch player 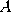 (if
(if 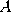 plays correctly).
plays correctly).
Task
Write a program that:
- reads from the standard input the description of a board and numbers of squares on which pieces are placed initially;
- decides if player
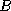 can catch player
can catch player 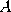 and if so,
computes how many turns he needs (we assume that both players play optimally);
and if so,
computes how many turns he needs (we assume that both players play optimally);
- writes the result to the standard output.
Input
In the first line of the standard input there are four integers  ,
, 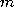 ,
,  and
and 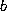 separated by single spaces,
where
separated by single spaces,
where 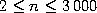 ,
, 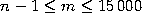 ,
, 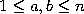 and
and 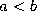 .
These are (respectively): the number of squares of the board,
the number of adjacent (unordered) pairs,
the number of the square on which the piece of player
.
These are (respectively): the number of squares of the board,
the number of adjacent (unordered) pairs,
the number of the square on which the piece of player 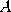 is placed,
the number of the square on which the piece of player
is placed,
the number of the square on which the piece of player 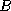 is placed.
is placed.
In each of the following 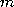 lines there are two distinct positive integers separated by a single space,
which donote numbers of adjacent squares.
lines there are two distinct positive integers separated by a single space,
which donote numbers of adjacent squares.
Output
In the first and only line of the standard output there should be:
- one word NIE (which means “no” in Polish), if player
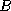 cannot catch player
cannot catch player 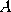 , or
, or
- one integer — the number of turns needed by
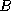 to catch
to catch 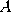 (if
(if 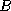 can catch
can catch 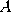 ).
).
Example
For the input data:
9 11 9 4 1 2 3 2 1 4 4 7 7 5 5 1 6 9 8 5 9 8 5 3 4 8
the correct result is:
3
Task author: Adam Borowski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English