
Zadanie Najazd (naj)
Pomóż nam usprawnić bazę zadań!
The Invasion
Memory limit: 32 MB
And so it has come - the Triangles have invaded Byteotia!
Byteotia lies on an island, occupying its entire surface.
The shape of the island is a convex polygon
(i.e. a polygon whose each inner angle is smaller than 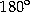 ).
A certain number of software factories are located in Byteotia, each of which generates constant gains or losses.
).
A certain number of software factories are located in Byteotia, each of which generates constant gains or losses.
The Triangles have decided to occupy such a part of Byteotia which:
- is a triangle-shaped area, the vertices of which are three different vertices of the polygon-island,
- brings the largest income i.e. the sum of all gains and losses generated by factories within the occupied area is maximal.
We assume that a factory located on the border or in the vertex of occupied area belongs to that area. A territory which contains no factory brings, obviously, a zero income.
Byteasar, the King of Byteotia, is concerned by the amount of losses the Triangles' invasion could generate. Help him by writing a programme which shall calculate the sum of gains and losses generated by factories which the Triangles wish to capture.
Task
Write a programme which:
- reads a decription of Byteotia's shape and the locations of factories from the input file,
- determines the maximal value of sum of all gains and losses generated by factories within a triangle, whose vertices are three different vertices of the polygon island,
- writes the outcome to the output file.
Input
The first line of the input file contains a single integer  (
(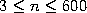 ),
denoting the number of vertices of the polygon-island.
The following
),
denoting the number of vertices of the polygon-island.
The following  lines of the input contain two integers each
lines of the input contain two integers each 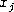 and
and 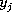 (
(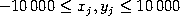 ), separated by a single space, denoting the
coordinates
), separated by a single space, denoting the
coordinates  and
and 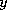 of consecutive vertices of the island, in a clockwise order.
The
of consecutive vertices of the island, in a clockwise order.
The 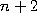 -nd line contains a single integer
-nd line contains a single integer 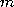 (
(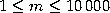 ), denoting the
total number of factories.
In each of the following
), denoting the
total number of factories.
In each of the following 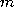 lines there are three integers
lines there are three integers 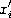 ,
, 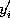 and
and 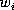 (
(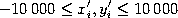 ,
, 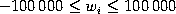 ), separated by
single spaces, denoting: the coordinates
), separated by
single spaces, denoting: the coordinates  and
and 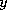 of the
of the 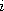 -th factory and
the gain (for
-th factory and
the gain (for 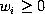 ) or loss (for
) or loss (for 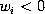 ) this factory generates, respectively.
Each factory is situated on the polygon-island i.e. within or on the border of it.
Distinct factories may be located in the same place i.e. have the same coordinates.
) this factory generates, respectively.
Each factory is situated on the polygon-island i.e. within or on the border of it.
Distinct factories may be located in the same place i.e. have the same coordinates.
Output
The first and only line of the output file should contain a single integer denoting the maximal value of sum of all gains and losses generated by factories within a triangle whose vertices are three different vertices of the polygon-island. Notice that it may happen that the outcome is a negative integer.
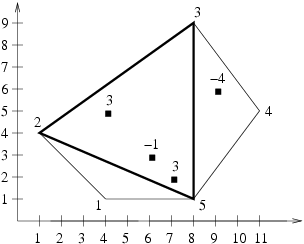
Example
For the input data:
5 4 1 1 4 8 9 11 5 8 1 4 7 2 3 6 3 -1 4 5 3 9 6 -4
the correct result is:
5
Task author: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English