
Zadanie Piloci (pil)
Pomóż nam usprawnić bazę zadań!
Piloci
Limit pamięci: 64 MB
Piloci w Bajtockim Ośrodku Treningowym przygotowują się do pełnienia misji wymagających niezwykłej precyzji i opanowania.
Miernikiem sukcesu jest uzyskanie możliwie długiego lotu wzdłuż zadanej trasy bez zbytnich odchyleń -
chodzi o utrzymanie w miarę równego kursu.
Jest to zadanie trudne, gdyż symulator jest tak czuły, że rejestruje najmniejsze nawet ruchy
wolanta1.
Zapisuje przy tym jeden parametr zwany wychyleniem.
Przed każdym eksperymentem treningowym piloci mają ustawiony poziom tolerancji 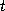 ;
ich celem jest wykonanie możliwie długiego fragmentu lotu o tej własności, że wszystkie
pomiary wychyleń w tym czasie będą różniły się nie więcej niż o
;
ich celem jest wykonanie możliwie długiego fragmentu lotu o tej własności, że wszystkie
pomiary wychyleń w tym czasie będą różniły się nie więcej niż o 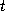 .
Innymi słowy, fragment lotu od momentu
.
Innymi słowy, fragment lotu od momentu 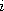 do momentu
do momentu 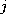 uznamy za mieszczący się w ramach tolerancji
uznamy za mieszczący się w ramach tolerancji 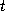 ,
jeśli wychylenia, począwszy od
,
jeśli wychylenia, począwszy od 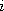 -tego pomiaru a skończywszy na
-tego pomiaru a skończywszy na 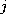 -tym, tworzą taki ciąg
-tym, tworzą taki ciąg 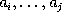 ,
że dla każdych
,
że dla każdych 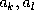 z tego ciągu zachodzi
z tego ciągu zachodzi 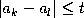 .
.
Twoim zadaniem jest napisanie programu, który na podstawie tolerancji 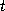 i ciągu pomiarów wychyleń wyznaczy długość
najdłuższego fragmentu tego ciągu mieszczącego się w ramach zadanej tolerancji.
i ciągu pomiarów wychyleń wyznaczy długość
najdłuższego fragmentu tego ciągu mieszczącego się w ramach zadanej tolerancji.
Wejście
W pierwszym wierszu standardowego wejścia zapisane są dwie liczby całkowite 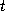 oraz
oraz  (
(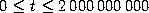 ,
, 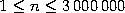 ), oddzielone pojedynczym odstępem
i określające poziom tolerancji oraz liczbę dokonanych pomiarów wychyleń.
W drugim wierszu znajdują się pooddzielane pojedynczymi odstępami wartości zmierzonych
wychyleń, będące liczbami całkowitymi z zakresu od
), oddzielone pojedynczym odstępem
i określające poziom tolerancji oraz liczbę dokonanych pomiarów wychyleń.
W drugim wierszu znajdują się pooddzielane pojedynczymi odstępami wartości zmierzonych
wychyleń, będące liczbami całkowitymi z zakresu od 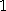 do
do 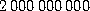 .
.
Wyjście
Twój program powinien wypisać w pierwszym i jedynym wierszu standardowego wyjścia jedną liczbę całkowitą: maksymalną długość fragmentu lotu mieszczącego się w ramach zadanej tolerancji.
Przykład
Dla danych wejściowych:
3 9 5 1 3 5 8 6 6 9 10
poprawną odpowiedzią jest:
4
Wyjaśnienie do przykładu: Mamy dwa najdłuższe fragmenty, oba długości 4: 5, 8, 6, 6 oraz 8, 6, 6, 9.
1. urządzenie sterujące w lotnictwie
Autor zadania: Piotr Chrząstowski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English