
Zadanie Wąż (waz)
Pomóż nam usprawnić bazę zadań!
Number of users: 28
Number of users with 100 points: 1
Average result: 34.2857
Snake
Memory limit: 512 MB
A snake fills a 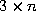 board completely.
Successive segments of the snake are numbered from
board completely.
Successive segments of the snake are numbered from 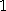 to
to 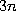 .
The segments with successive numbers (i.e., 1 and 2, 2 and 3, 3 and 4...) occupy squares
that share an edge.
For example, a snake can fill a
.
The segments with successive numbers (i.e., 1 and 2, 2 and 3, 3 and 4...) occupy squares
that share an edge.
For example, a snake can fill a 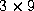 board as follows:
board as follows:
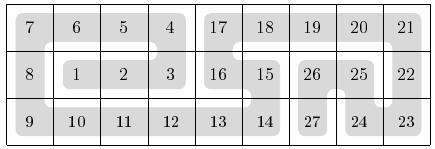
The snake's segment numbers in some of the squares have been erased. Can you reconstruct the snake?
Input
In the first line of the standard input, there is a single integer  (
(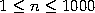 ), the length of the board.
The three lines that follow describe the board;
the
), the length of the board.
The three lines that follow describe the board;
the 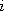 -th of them contains
-th of them contains  integers
integers 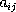 (
(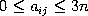 for
for 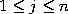 ).
If
).
If 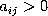 , then
, then 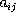 is the number of the snake's segment
occupying the
is the number of the snake's segment
occupying the 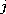 -th square of the
-th square of the 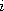 -th row of the board.
If on the other hand
-th row of the board.
If on the other hand 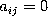 , then the number of the snake's segment
on this square is unknown.
, then the number of the snake's segment
on this square is unknown.
In tests worth 15% of the total score 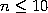 holds,
in those worth 40% of the total score
holds,
in those worth 40% of the total score 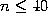 holds,
and finally, in those worth 70% of the total score
holds,
and finally, in those worth 70% of the total score 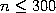 holds.
holds.
Output
Your program is to print three lines to the standard output.
The 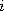 -th lines should hold
-th lines should hold  positive integers
positive integers 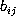 (for
(for 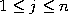 ).
All the numbers
).
All the numbers 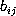 together should be a permutation of the numbers from
together should be a permutation of the numbers from 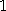 to
to 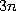 .
The output numbers should be a valid reconstruction of the snake, i.e., they should
be consistent with the (positive) input numbers and satisfy aforementioned constraints.
.
The output numbers should be a valid reconstruction of the snake, i.e., they should
be consistent with the (positive) input numbers and satisfy aforementioned constraints.
You may assume that there is at least one valid reconstruction of the snake. If there is more than one, your program can print any valid reconstruction.
Example
For the input data:
9 0 0 5 0 17 0 0 0 21 8 0 0 3 16 0 0 25 0 0 0 0 0 0 0 0 0 23
the correct result is:
7 6 5 4 17 18 19 20 21 8 1 2 3 16 15 26 25 22 9 10 11 12 13 14 27 24 23
Task author: Jakub Radoszewski.
<Submit a solution> [0/100]Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English