
Zadanie Permutacja [B] (per)
Pomóż nam usprawnić bazę zadań!
Permutation [B]
Memory limit: 32 MB
You are given a sequence of positive integers 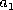 ,
, 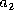 , ...,
, ..., 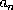 .
We would like to order the numbers from
.
We would like to order the numbers from 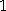 to
to  in such a way, that the
in such a way, that the 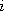 -th number is not greater than
-th number is not greater than 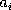 (for each
(for each 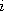 ).
In other words, we are looking for a permutation
).
In other words, we are looking for a permutation 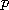 of numbers from
of numbers from 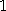 to
to  , which satisfies:
, which satisfies: 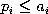 for each
for each 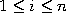 .
There is one more problem, the sequence
.
There is one more problem, the sequence 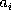 may change over time...
may change over time...
Input
The first line of standard input contains one integer  (
(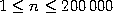 ), the number of elements of the
), the number of elements of the 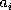 sequence.
In the second line, there is a sequence of
sequence.
In the second line, there is a sequence of  positive integers
positive integers 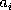 (
(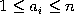 ), separated by single spaces.
The third line contains one integer
), separated by single spaces.
The third line contains one integer 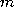 (
( ), representing the number of modifications made to the
), representing the number of modifications made to the 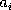 sequence.
The following
sequence.
The following 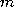 lines describe these modifications.
Each description consists of two integers
lines describe these modifications.
Each description consists of two integers 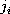 and
and 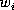 (
(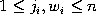 for
for 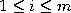 ),
separated by single spaces and meaning that
),
separated by single spaces and meaning that 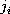 -th element of the sequence becomes
-th element of the sequence becomes 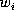 .
The operations take place in turns, so the
.
The operations take place in turns, so the 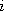 -th modification is applied to the sequence
altered by
-th modification is applied to the sequence
altered by 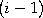 previous modifications.
previous modifications.
Output
Your program should output exactly 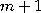 lines to the standard output.
Each of those lines should contain one word TAK (meaning YES) or NIE (meaning NO).
The word in the first line should tell if there exists a permutation
lines to the standard output.
Each of those lines should contain one word TAK (meaning YES) or NIE (meaning NO).
The word in the first line should tell if there exists a permutation 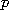 , which satisfies
, which satisfies
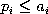 for each
for each 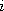 (for the original
(for the original 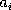 sequence), whereas the words from
following lines answer the question whether there exist any (potentially different)
permutations that satisfy the given conditions for the
sequence), whereas the words from
following lines answer the question whether there exist any (potentially different)
permutations that satisfy the given conditions for the 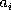 sequence after each
modification.
sequence after each
modification.
Example
For the input data:
5 3 4 3 2 5 2 5 4 1 5
the correct result is:
TAK NIE TAK
Explanation of the example.
For the original 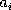 sequence, the condition is satisfied by permutation
sequence, the condition is satisfied by permutation 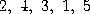 .
After the first modification, the sequence becomes
.
After the first modification, the sequence becomes 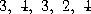 and for this sequence
no valid permutation exists.
After the second modification, the sequence is
and for this sequence
no valid permutation exists.
After the second modification, the sequence is 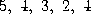 .
An example of a permutation
.
An example of a permutation 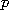 satisfying all constraints for this sequence is
satisfying all constraints for this sequence is 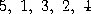 .
.
Task author: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English