
Zadanie Parking [B] (par)
Pomóż nam usprawnić bazę zadań!
Parking [B]
Limit pamięci: 128 MB
Zastanawialiście się kiedyś, jak wygląda praca parkingowego? Z pozoru nie wygląda to na trudną robotę: klienci zostawiają samochody, które trzeba zaparkować. Proste? Mogłoby się tak wydawać, ale rzeczywistość jest bardziej skomplikowana. Głównym problemem naszego parkingowego jest jego szef.
Pewnego dnia szef nakazał swojemu biednemu pracownikowi przestawić wszystkie samochody na parkingu zgodnie ze swoim widzimisię. Parkingowy, patrząc na kartkę, którą przyniósł mu szef, i na kartkę z aktualnym ustawieniem samochodów, zastanawia się, czy jest to w ogóle możliwe. Pomóż mu!
Parking reprezentujemy jako prostokąt (na płaszczyźnie) o wysokości  .
Dla wygody opisu zadajemy prostokątny układ współrzędnych o osiach równoległych do boków prostokąta.
Początek układu współrzędnych leży w lewym dolnym rogu prostokąta.
Parking jest na tyle szeroki, że wygodnie nam jest przyjąć, iż prawy bok prostokąta znajduje się nieskończenie daleko.
.
Dla wygody opisu zadajemy prostokątny układ współrzędnych o osiach równoległych do boków prostokąta.
Początek układu współrzędnych leży w lewym dolnym rogu prostokąta.
Parking jest na tyle szeroki, że wygodnie nam jest przyjąć, iż prawy bok prostokąta znajduje się nieskończenie daleko.
Samochody, dla ułatwienia, także uznajemy za prostokąty o bokach równoległych do osi układu współrzędnych. Bywają jednak samochody większe i mniejsze, dlatego odpowiadające im prostokąty mogą mieć różne rozmiary. Ustawienie samochodów na parkingu jest prawidłowe, jeżeli wszystkie samochody znajdują się na parkingu oraz żaden fragment tego parkingu nie jest zajęty przez dwa pojazdy jednocześnie. Dopuszczamy jednak, by brzegi prostokątów reprezentujących samochody nachodziły na siebie.
Parkingowy ma już spory staż pracy, dlatego może przemieszczać samochody w dowolny sposób w każdym kierunku (mówiąc formalnie: parkingowy może zawsze przesunąć dowolny samochód o dowolny wektor), byleby tylko samochody nie najechały na siebie. Nie może ich jednak obracać.
Twoim zadaniem jest określić, czy można przestawić samochody z aktualnej pozycji do pozycji ustalonej przez szefa, nie uszkadzając żadnego samochodu.
Wejście
W pierwszym wierszu wejścia podana jest liczba zestawów testowych  (
(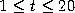 ), które opisane są kolejno w dalszej części wejścia.
Opis każdego zestawu testowego rozpoczyna się od wiersza zawierającego dwie liczby całkowite
), które opisane są kolejno w dalszej części wejścia.
Opis każdego zestawu testowego rozpoczyna się od wiersza zawierającego dwie liczby całkowite  ,
, 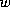 (
(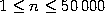 ,
,  ),
oznaczające liczbę samochodów na parkingu oraz wysokość prostokąta reprezentującego parking.
),
oznaczające liczbę samochodów na parkingu oraz wysokość prostokąta reprezentującego parking.
W kolejnych  wierszach znajduje się opis początkowego ustawienia samochodów:
wierszach znajduje się opis początkowego ustawienia samochodów:
 -ty z tych wierszy zawiera cztery liczby całkowite
-ty z tych wierszy zawiera cztery liczby całkowite  ,
,  ,
,  i
i  (
( ,
,  ),
które opisują prostokąt o przeciwległych wierzchołkach w punktach
),
które opisują prostokąt o przeciwległych wierzchołkach w punktach  i
i  , odpowiadający
, odpowiadający  -temu samochodowi na parkingu.
Wszystkie prostokąty mają dodatnie pole.
-temu samochodowi na parkingu.
Wszystkie prostokąty mają dodatnie pole.
W następnych  wierszach znajduje się opis docelowego ustawienia samochodów, podany w analogicznym formacie.
Samochody w obu opisach są podane w tej samej kolejności (
wierszach znajduje się opis docelowego ustawienia samochodów, podany w analogicznym formacie.
Samochody w obu opisach są podane w tej samej kolejności ( -ty samochód z opisu ustawienia początkowego odpowiada
-ty samochód z opisu ustawienia początkowego odpowiada  -temu samochodowi z opisu ustawienia docelowego).
Ten sam samochód może być opisany w ustawieniu docelowym za pomocą innych wierzchołków niż w ustawieniu początkowym.
Możesz założyć, że oba opisy są prawidłowe.
-temu samochodowi z opisu ustawienia docelowego).
Ten sam samochód może być opisany w ustawieniu docelowym za pomocą innych wierzchołków niż w ustawieniu początkowym.
Możesz założyć, że oba opisy są prawidłowe.
W testach wartych 5 punktów spełniony jest dodatkowy warunek  .
.
Wyjście
Na wyjście należy wypisać  wierszy:
wierszy:  -ty z nich powinien zawierać jedno słowo TAK lub NIE,
w zależności od tego, czy w
-ty z nich powinien zawierać jedno słowo TAK lub NIE,
w zależności od tego, czy w  -tym zestawie testowym da się przestawić samochody zgodnie z wymaganiami szefa.
-tym zestawie testowym da się przestawić samochody zgodnie z wymaganiami szefa.
Przykład
Dla danych wejściowych:
2 3 3 0 0 2 2 2 1 4 3 4 0 6 1 0 0 2 2 2 1 4 3 0 2 2 3 3 3 0 0 2 2 2 1 4 3 4 0 6 1 2 1 4 3 0 0 2 2 4 0 6 1
poprawną odpowiedzią jest:
TAK NIE

Wyjaśnienie do przykładu: Rysunek przedstawia pierwszy zestaw testowy z przykładu. W lewej części pokazano początkowe ustawienie samochodów, a w prawej - ustawienie docelowe. Aby samochód 3 wstawić w odpowiednie miejsce, samochód 2 należy przesunąć w dół lub w prawo. W drugim zestawie testowym musielibyśmy zamienić miejscami samochody 1 i 2, co nie jest możliwe.
Autorzy zadania: Jakub Łącki, Andrzej Grzywocz.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English