
Zadanie Liczby prof. Wesołka (lii)
Pomóż nam usprawnić bazę zadań!
Liczby Profesora Wesołka
Limit pamięci: 32 MB
Profesor Bajtazar Wesołek właśnie dostał niepowtarzalną szansę. Dowiedział się, że z Fundacji Pomocy Zakręconym Bajtoprofesorom może dostać okrągłe milion bajtków na swoje badania. Profesor zawsze stara się, aby jego badania były ciekawe i interesujące dla innych. W końcu ktoś dostrzegł jego ciężką pracę, a co jeszcze ważniejsze, dofinansuje ją!
Jednak sprawa nie jest taka prosta. Profesor dostał tylko tydzień czasu na przedstawienie dotychczasowych wynikó swoich badań, a oprócz opracowania wyników, musi również wypełnić całą stertę (albo stos - jak kto woli) podań i wniosków. Jak każdy ,,zakręcony'' naukowiec, profesor Wesołek jest trochę bałaganiarski. Wyniki jego prac gdzieś mu się zapodziały. Dlatego poprosił Ciebie o pomoc w napisaniu programu, który odtworzy te wyniki.
Jako że profesor nie lubi zanudzać swoich przyjaciół i współpracowników, nie badał pospolitych i nudnych całek, tylko pasjonujące wszystkich w jego otoczeniu liczby pierwsze.
Dla liczby pierwszej  większej od
większej od  , liczby naturalnej
, liczby naturalnej  większej
od 1 oraz liczby naturalnej
większej
od 1 oraz liczby naturalnej  mniejszej od
mniejszej od  , profesor
stwierdził, że liczba
, profesor
stwierdził, że liczba  jest
jest 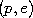 -ciekawa, jeśli istnieje liczba
naturalna
-ciekawa, jeśli istnieje liczba
naturalna  , taka że
, taka że  czyli gdy
czyli gdy  oraz
oraz  dają taką samą resztę przy dzieleniu przez
dają taką samą resztę przy dzieleniu przez  .
.
Zadanie
Napisz program, który:
- wczyta liczbę pierwszą
 , wykładnik
, wykładnik  oraz
pewien ciąg liczb,
oraz
pewien ciąg liczb,
- dla każdej liczby z tego ciągu sprawdzi,
czy jest ona
 -ciekawa,
-ciekawa,
- wypisze wynik.
Wejście
W pierwszym wierszu znajdują się dwie liczby oddzielone
pojedynczym odstępem: liczba pierwsza  i liczba naturalna
i liczba naturalna  - liczby wybrane przez profesora do badań,
- liczby wybrane przez profesora do badań,
 . W drugim wierszu znajduje się
jedna liczba naturalna
. W drugim wierszu znajduje się
jedna liczba naturalna  - liczba przypadków do rozważenia,
- liczba przypadków do rozważenia,
 . W każdym z kolejnych
. W każdym z kolejnych  wierszy zapisana
jest jedna liczba całkowita. W
wierszy zapisana
jest jedna liczba całkowita. W  -tym z tych wierszy zapisano
liczbę
-tym z tych wierszy zapisano
liczbę  ,
,  .
.
Wyjście
Twój program powinien wypisać dokładnie  wierszy.
W
wierszy.
W 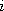 -tym (
-tym ( ) wierszu powinno się znajdować
dokładnie jedno słowo - TAK, jeśli liczba
) wierszu powinno się znajdować
dokładnie jedno słowo - TAK, jeśli liczba  jest
jest
 -ciekawa, NIE w przeciwnym wypadku.
-ciekawa, NIE w przeciwnym wypadku.
Przykład
Dla danych wejściowych:17 2 5 1 9 3 7 6poprawną odpowiedzią jest:
TAK TAK NIE NIE NIE
Autorzy zadania: Jakub Pawlewicz, Jakub Radoszewski (treść: Szymon Wąsik).
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English