
Zadanie Podatek (pod)
Pomóż nam usprawnić bazę zadań!
Podatek
Limit pamięci: 128 MB
Władca królestwa Bajtocji, podążając za ogólnoświatowym trendem, postanowił opodatkować wszystko, co się da. Ostatnio wprowadzoną daniną jest tzw. podatek podróżny, który musi płacić każdy, kto przemieszcza się po kraju.
Każdej bajtockiej drodze przypisana jest pewna stawka podatku. Gdy podczas podróży po Bajtocji przejeżdżamy przez miasto, musimy zapłacić w tamtejszym urzędzie podatek, który obliczany jest jako maksimum ze stawki obowiązującej na drodze, którą wjechaliśmy do miasta, oraz stawki na drodze, którą z miasta wyjedziemy. Płaci się też w początkowym i docelowym mieście na trasie podróży - wtedy, obliczając podatek, bierze się pod uwagę tylko jedną drogę.
Twój przyjaciel Bajtazar wybiera się w podróż z Bajtowa do Bajtawy. Pomóż mu tak zaplanować trasę przejazdu, żeby zapłacił jak najniższy podatek.
Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite  oraz
oraz 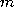 (
(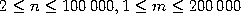 ), oznaczające odpowiednio liczbę miast oraz liczbę
dróg w Bajtocji. Miasta są ponumerowane liczbami od
), oznaczające odpowiednio liczbę miast oraz liczbę
dróg w Bajtocji. Miasta są ponumerowane liczbami od  do
do  .
.
Kolejne 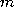 wierszy zawiera opisy dróg: w
wierszy zawiera opisy dróg: w 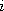 -tym z tych wierszy znajdują się trzy liczby całkowite
-tym z tych wierszy znajdują się trzy liczby całkowite
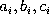 (
(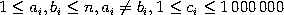 ).
Oznaczają one, że miasta
).
Oznaczają one, że miasta 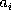 i
i 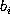 są połączone dwukierunkową drogą, na której
obowiązująca stawka podatku wynosi
są połączone dwukierunkową drogą, na której
obowiązująca stawka podatku wynosi 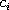 bajtalarów.
Pomiędzy dowolną parą miast istnieje co najwyżej jedna droga.
bajtalarów.
Pomiędzy dowolną parą miast istnieje co najwyżej jedna droga.
Wyjście
Pierwszy i jedyny wiersz wyjścia powinien zawierać jedną liczbę całkowitą -
minimalny koszt podróży (w bajtalarach) z Bajtowa (miasta oznaczonego numerem 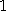 )
do Bajtawy (miasta oznaczonego numerem
)
do Bajtawy (miasta oznaczonego numerem  ). Możesz założyć, że zawsze
istnieje ciąg dróg łączący te miasta.
). Możesz założyć, że zawsze
istnieje ciąg dróg łączący te miasta.
Przykład
Dla danych wejściowych:
4 5 1 2 5 1 3 2 2 3 1 2 4 4 3 4 8
poprawną odpowiedzią jest:
12
Wyjaśnienie do przykładu:
W powyższym przykładzie optymalna trasa wiedzie przez miasta 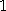 ,
, 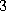 ,
, 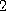 oraz
oraz  . Kolejno zapłacimy w nich podatek w wysokości
. Kolejno zapłacimy w nich podatek w wysokości 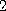 ,
, 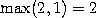 ,
,
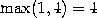 oraz
oraz  , co łącznie daje
, co łącznie daje 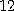 bajtalarów.
bajtalarów.
Autor zadania: Jakub Łącki (i nie tylko).
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English