
Zadanie Bramki XOR (xor)
Pomóż nam usprawnić bazę zadań!
Bramki XOR
Limit pamięci: 32 MB
Każda bramka XOR ma dwa wejścia i jedno wyjście, a jej działanie opisuje następująca tabelka:
wejście 1 wejście 2 wyjście
0 0 0
0 1 1
1 0 1
1 1 0
Siecią XOR nazywamy układ bramek XOR, mający  wejść i jedno wyjście, spełniający następujące warunki:
wejść i jedno wyjście, spełniający następujące warunki:
- Każde wejście sieci XOR jest połączone z przynajmniej jednym wejściem bramki.
- Każde wejście każdej bramki jest połączone z jednym wejściem sieci albo z jednym wyjściem innej bramki.
- Wyjście dokładnie jednej bramki jest połączone z wyjściem sieci.
- Każde wyjście bramki w sieci jest połączone z przynajmniej jednym wejściem innej bramki albo z jedynym wyjściem sieci.
- Istnieje taka numeracja bramek, że do każdego wejścia dowolnej bramki jest podłączone wejście sieci albo wyjście bramki o mniejszym numerze.
Przykład

Przedstawiony na rysunku układ 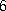 bramek mający
bramek mający 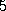 wejść i
wejść i 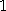 wyjście spełnia warunki 1–5,
więc jest siecią XOR.
Uwaga: bramki na rysunku zostały ponumerowane dowolnie, ale istnieje numeracja spełniająca warunek określony w punkcie 5.
wyjście spełnia warunki 1–5,
więc jest siecią XOR.
Uwaga: bramki na rysunku zostały ponumerowane dowolnie, ale istnieje numeracja spełniająca warunek określony w punkcie 5.
Wszystkie wejścia sieci są ponumerowane od 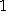 do
do  .
Stan wejść sieci XOR opisuje słowo wejściowe utworzone z
.
Stan wejść sieci XOR opisuje słowo wejściowe utworzone z  cyfr dwójkowych
cyfr dwójkowych 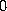 i
i 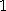 — przyjmujemy,
że
— przyjmujemy,
że 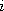 -ta od lewej cyfra danego słowa wejściowego, to stan
-ta od lewej cyfra danego słowa wejściowego, to stan  -tego wejścia sieci.
Dla dowolnego stanu wejść sieć daje na wyjściu
-tego wejścia sieci.
Dla dowolnego stanu wejść sieć daje na wyjściu 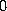 albo
albo 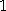 .
Każde słowo wejściowe jest dwójkowym zapisem jakiejś liczby naturalnej,
więc słowa te można uporządkować zgodnie z ich wartościami liczbowymi.
Sieci XOR będziemy testowali podając na wejściu kolejne słowa z ustalonego zakresu i zliczając liczbę otrzymanych w wyniku jedynek.
.
Każde słowo wejściowe jest dwójkowym zapisem jakiejś liczby naturalnej,
więc słowa te można uporządkować zgodnie z ich wartościami liczbowymi.
Sieci XOR będziemy testowali podając na wejściu kolejne słowa z ustalonego zakresu i zliczając liczbę otrzymanych w wyniku jedynek.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia opis sieci XOR:
liczbę wejść
 , liczbę bramek
, liczbę bramek 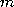 , numer bramki połączonej z wyjściem sieci oraz opisy połączeń,
a następnie dwa
, numer bramki połączonej z wyjściem sieci oraz opisy połączeń,
a następnie dwa  -bitowe słowa wejściowe — dolne i górne ograniczenie zakresu, w jakim będziemy testowali sieć,
-bitowe słowa wejściowe — dolne i górne ograniczenie zakresu, w jakim będziemy testowali sieć,
- oblicza liczbę jedynek otrzymanych na wyjściu sieci dla słów wejściowych z danego zakresu,
- zapisuje wynik na standardowe wyjście.
Zakładamy, że: 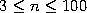 ,
, 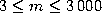 oraz, że bramki danej sieci są ponumerowane w dowolnym porządku liczbami od
oraz, że bramki danej sieci są ponumerowane w dowolnym porządku liczbami od  do
do 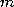 .
.
Wejście
W pierwszym wierszu standardowego wejścia są zapisane trzy liczby całkowite dodatnie pooddzielane pojedynczym odstępem.
Jest to liczba wejść  danej sieci XOR, liczba bramek
danej sieci XOR, liczba bramek 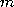 oraz numer bramki połączonej z wyjściem sieci.
oraz numer bramki połączonej z wyjściem sieci.
W kolejnych 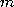 wierszach znajdują się opisy połączeń bramek sieci.
W
wierszach znajdują się opisy połączeń bramek sieci.
W 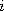 -tym z tych wierszy, dla
-tym z tych wierszy, dla 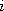 od
od 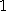 do
do 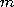 , znajduje się opis połączeń dwóch wejść bramki o numerze
, znajduje się opis połączeń dwóch wejść bramki o numerze  ,
który ma postać dwóch liczb całkowitych nie mniejszych niż
,
który ma postać dwóch liczb całkowitych nie mniejszych niż 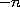 i nie większych niż
i nie większych niż 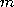 , oddzielonych pojedynczym odstępem.
Jeśli odpowiednie wejście do bramki jest połączone z wejściem do sieci o numerze
, oddzielonych pojedynczym odstępem.
Jeśli odpowiednie wejście do bramki jest połączone z wejściem do sieci o numerze 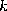 , to opisem tego połączenia jest liczba ujemna
, to opisem tego połączenia jest liczba ujemna 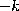 ,
a jeśli wejście do bramki jest połączone z wyjściem innej bramki o numerze
,
a jeśli wejście do bramki jest połączone z wyjściem innej bramki o numerze 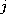 , to opisem tego połączenia jest liczba dodatnia
, to opisem tego połączenia jest liczba dodatnia 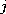 .
.
W kolejnych dwóch wierszach są zapisane dwa  -bitowe słowa
-bitowe słowa  oraz
oraz 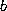 .
Jest to dolne i górne ograniczenie zakresu testowania sieci.
Zakładamy, że w danym zakresie mieści się nie więcej niż
.
Jest to dolne i górne ograniczenie zakresu testowania sieci.
Zakładamy, że w danym zakresie mieści się nie więcej niż 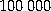 słów.
słów.
Wyjście
Na standardowe wyjście należy zapisać jedną liczbę całkowitą nieujemną — liczbę jedynek,
jakie powinniśmy otrzymać na wyjściu poprawnie działającej danej sieci XOR dla słów wejściowych  z danego zakresu:
z danego zakresu:
 , gdzie nierówność
, gdzie nierówność  należy rozumieć jako relację porządku zgodnego z wartościami liczbowymi słów dwójkowych.
należy rozumieć jako relację porządku zgodnego z wartościami liczbowymi słów dwójkowych.
Przykład
Dla danych wejściowych:
5 6 5 -1 -2 1 3 1 -2 2 -3 4 6 -4 -5 00111 01110
poprawną odpowiedzią jest:
5
Autor zadania: Tomasz Śmigielski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English