
Zadanie Kurort narciarski (kur)
Pomóż nam usprawnić bazę zadań!
Kurort narciarski
Limit pamięci: 32 MB
W Bajtogórach znajduje się kurort narciarski Bajtyrk słynący z narciarskich tras biegowych. Są one bardzo malownicze, gdyż część z nich jest położona wysoko w górach lub w trudno dostępnych miejscach. Użytkownicy tras często korzystają z wyciągów ułatwiających dotarcie do niektórych z nich. Każdy wyciąg i każda trasa zaczyna się i kończy na określonej polanie. Trasy narciarskie nie mogą się przecinać, ale mogą przebiegać naturalnymi skalnymi tunelami i estakadami.
Trasy narciarskie mogą być jednokierunkowe lub dwukierunkowe. Podobnie, niektóre wyciągi (kolejki linowe) mogą być jedno lub dwukierunkowe.
Za korzystanie z wyciągów płaci się kartą magnetyczną. Karty kupuje się w kasach. Każda karta zawiera określoną liczbę punktów. Skorzystanie z każdego z wyciągów wiąże się z utratą pewnej liczby punktów zależnej od wyciągu. Niestety kasy nie zwracają pieniędzy za niewykorzystane punkty.
Bajtoni jest dziś na nartach ostatni dzień. Została mu jedna karta z pewną liczbą punktów, które chciałby wykorzystać do maksimum. Możesz założyc, że ta liczba punktów wystarczy na powrót do Bajtyrku.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opis sieci tras i wyciągów oraz informacje o położeniu Bajtoniego i liczbie punktów na jego karcie,
- obliczy, z jaką najmniejszą liczbą punktów na karcie Bajtoni może dziś wrócić na dół, do Bajtyrku,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia zapisane są dwie dodatnie liczby całkowite
 i
i 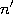 ,
,  , oddzielone pojedynczym odstępem,
oznaczające odpowiednio liczbę wszystkich polan oraz liczbę tych polan, które
znajdują się na dole w samym Bajtyrku (są to polany o numerach od
, oddzielone pojedynczym odstępem,
oznaczające odpowiednio liczbę wszystkich polan oraz liczbę tych polan, które
znajdują się na dole w samym Bajtyrku (są to polany o numerach od  do
do 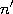 włącznie).
włącznie).
W drugim wierszu zapisana jest jedna dodatnia liczba całkowita 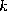 ,
,
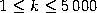 , równa łącznej liczbie wszystkich tras narciarskich.
Każdy z kolejnych
, równa łącznej liczbie wszystkich tras narciarskich.
Każdy z kolejnych 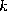 wierszy zawiera po dwie różne dodatnie liczby
całkowite, pooddzielane pojedynczymi odstępami,
wierszy zawiera po dwie różne dodatnie liczby
całkowite, pooddzielane pojedynczymi odstępami, 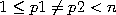 .
Liczby te oznaczają numer początkowej i końcowej polany danej trasy narciarskiej.
Trasy dwukierunkowe są tu liczone dwukrotnie i reprezentowane w pliku wejściowym przez
dwa (niekoniecznie kolejne) wiersze (postaci "
.
Liczby te oznaczają numer początkowej i końcowej polany danej trasy narciarskiej.
Trasy dwukierunkowe są tu liczone dwukrotnie i reprezentowane w pliku wejściowym przez
dwa (niekoniecznie kolejne) wiersze (postaci "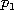
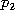 " i "
" i "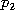
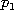 ").
").
W 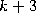 -cim wierszu zapisana jest jedna dodatnia liczba całkowita
-cim wierszu zapisana jest jedna dodatnia liczba całkowita
 ,
,  , równa liczbie wszystkich wyciągów.
W kolejnych
, równa liczbie wszystkich wyciągów.
W kolejnych 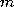 wierszach opisane są wyciągi. W każdym z tych wierszy
zapisane są trzy dodatnie liczby całkowite
wierszach opisane są wyciągi. W każdym z tych wierszy
zapisane są trzy dodatnie liczby całkowite 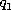 ,
, 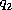 i
i  ,
pooddzielane pojedynczymi odstępami. Liczby
,
pooddzielane pojedynczymi odstępami. Liczby 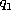 i
i 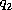 oznaczają
odpowiednio numer polany, na której wyciąg się zaczyna i numer polany, na której się
kończy,
oznaczają
odpowiednio numer polany, na której wyciąg się zaczyna i numer polany, na której się
kończy, 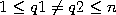 . Liczba
. Liczba  jest równa liczbie punktów,
które trzeba zapłacić za przejazd wyciągiem,
jest równa liczbie punktów,
które trzeba zapłacić za przejazd wyciągiem,  . Wyciągi
dwukierunkowe (kolejki linowe) są tu liczone dwukrotnie i reprezentowane w pliku wejściowym
przez dwa (niekoniecznie kolejne) wiersze (postaci "
. Wyciągi
dwukierunkowe (kolejki linowe) są tu liczone dwukrotnie i reprezentowane w pliku wejściowym
przez dwa (niekoniecznie kolejne) wiersze (postaci "
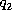
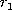 " i
"
" i
"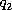
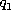
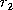 ").
Ceny przejazdu wyciągiem w jedną i w drugą stronę mogą być różne.
").
Ceny przejazdu wyciągiem w jedną i w drugą stronę mogą być różne.
W ostatnim wierszu zapisane są dwie dodatnie liczby całkowite 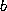 i
i  ,
oddzielone pojedynczym odstępem,
,
oddzielone pojedynczym odstępem, 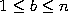 ,
,  .
Pierwsza z nich oznacza numer polany, na której znajduje się Bajtoni
a druga jest równa liczbie punktów na jego ostatniej karcie magnetycznej.
.
Pierwsza z nich oznacza numer polany, na której znajduje się Bajtoni
a druga jest równa liczbie punktów na jego ostatniej karcie magnetycznej.
Wyjście
Twój program powinien zapisać w pierwszym (i jedynym) wierszu standardowego wyjścia jedną liczbę całkowitą, równą najmniejszej możliwej liczbie punktów, z jaką Bajtoni może wrócić do Bajtyrku.
Przykład
Dla danych wejściowych:
5 2 6 3 2 3 5 1 5 3 4 1 2 4 3 4 3 1 1 4 3 5 5 2 2 3 4 5 4 9
Dla danych wejściowych:
1
Autor zadania: Marcin Sawicki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English