
Zadanie Uczta (ucz)
Pomóż nam usprawnić bazę zadań!
Uczta
Limit pamięci: 64 MB
Król Bajtazar organizuje wielką ucztę z okazji swoich 128. urodzin.
Postanowił zaproszonych gości usadzić przy okrągłych stołach tak,
żeby żaden z gości nie siedział przy stole sam.
Wybrał już  osób, które mógłby zaprosić na przyjęcie.
Następnie uszeregował gości w kolejności od najważniejszych i ponumerował ich kolejno od
osób, które mógłby zaprosić na przyjęcie.
Następnie uszeregował gości w kolejności od najważniejszych i ponumerował ich kolejno od  do
do  (gość numer
(gość numer  jest najważniejszy).
jest najważniejszy).
Goście są bardzo wymagający: każdy z nich podał królowi wymagania odnośnie do tego,
kto może siedzieć po jego prawej stronie.
Król chce, aby każdy z zaproszonych gości miał dogodne towarzystwo, toteż nie pozwoli, aby wymagania któregoś z gości nie zostały spełnione.
Może się więc okazać, że nie uda się zaprosić wszystkich  osób.
Bajtazar poprosił Ciebie (nadwornego informatyka) o wyznaczenie najlepszego
z możliwych zbiorów zaproszonych gości i przykładowego usadzenia ich przy okrągłych stołach.
Król, spytany o to, co miał na myśli, mówiąc o najlepszym zbiorze gości,
odpowiedział zaskakująco rzeczowo, jak na
osób.
Bajtazar poprosił Ciebie (nadwornego informatyka) o wyznaczenie najlepszego
z możliwych zbiorów zaproszonych gości i przykładowego usadzenia ich przy okrągłych stołach.
Król, spytany o to, co miał na myśli, mówiąc o najlepszym zbiorze gości,
odpowiedział zaskakująco rzeczowo, jak na  -letniego informatycznego laika:
-letniego informatycznego laika:
Aby porównać dwa zbiory gości, wybieram osobę o najmniejszym numerze, która należy do dokładnie jednego z porównywanych zbiorów. Ta właśnie osoba należy do lepszego zbioru.
Przy tak określonym porządku można faktycznie jednoznacznie określić, który z potencjalnych zbiorów gości jest najlepszy.
Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita  (
( )
oznaczająca liczbę gości.
W
)
oznaczająca liczbę gości.
W  -tym z kolejnych
-tym z kolejnych  wierszy znajduje się opis preferencji osoby o numerze
wierszy znajduje się opis preferencji osoby o numerze  .
Opis preferencji rozpoczyna się od liczby całkowitej
.
Opis preferencji rozpoczyna się od liczby całkowitej  (
( ).
Po niej następuje
).
Po niej następuje  parami różnych
numerów osób - są to liczby całkowite z zakresu od
parami różnych
numerów osób - są to liczby całkowite z zakresu od  do
do  , różne od
, różne od  .
Każda taka liczba określa jedną osobę, która może usiąść po prawicy osoby numer
.
Każda taka liczba określa jedną osobę, która może usiąść po prawicy osoby numer  .
Suma liczb
.
Suma liczb  nie przekracza
nie przekracza  .
.
W testach wartych  punktów zachodzi dodatkowo warunek: jeśli osoba
punktów zachodzi dodatkowo warunek: jeśli osoba  zezwala na posadzenie
osoby
zezwala na posadzenie
osoby  po swojej prawej stronie, to również osoba
po swojej prawej stronie, to również osoba  zezwala na posadzenie osoby
zezwala na posadzenie osoby
 po swojej prawej stronie.
W szczególności oznacza to, że te dwie osoby mogą usiąść razem przy jednym, dwuosobowym stole.
po swojej prawej stronie.
W szczególności oznacza to, że te dwie osoby mogą usiąść razem przy jednym, dwuosobowym stole.
W testach wartych  punktów da się zaprosić wszystkie
punktów da się zaprosić wszystkie  osób na przyjęcie.
osób na przyjęcie.
Wyjście
W pierwszym wierszu wyjścia powinna znaleźć się liczba całkowita  ,
oznaczająca liczbę stołów w znalezionym rozwiązaniu.
Następne
,
oznaczająca liczbę stołów w znalezionym rozwiązaniu.
Następne  wierszy powinno zawierać opisy poszczególnych stołów.
Opis stołu rozpoczyna się od liczby całkowitej
wierszy powinno zawierać opisy poszczególnych stołów.
Opis stołu rozpoczyna się od liczby całkowitej  oznaczającej liczbę gości przy nim siedzących.
Dalej następuje
oznaczającej liczbę gości przy nim siedzących.
Dalej następuje  liczb oznaczających ich numery.
Numery gości powinny być podawane kolejno, w porządku przeciwnym do kierunku ruchu wskazówek zegara.
Pierwszy z wypisanych gości będzie siedział po prawej stronie ostatniego z gości.
liczb oznaczających ich numery.
Numery gości powinny być podawane kolejno, w porządku przeciwnym do kierunku ruchu wskazówek zegara.
Pierwszy z wypisanych gości będzie siedział po prawej stronie ostatniego z gości.
Przykład
Dla danych wejściowych:
6 3 2 6 3 0 1 4 1 1 1 4 1 5
poprawną odpowiedzią jest:
1 3 1 3 4
W powyższym przykładzie lepiej zaprosić na ucztę osoby  ,
, 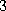 oraz
oraz  niż osoby
niż osoby  ,
,  ,
,  oraz
oraz  .
Zgodnie z kryterium króla lepszy zbiór wyznacza osoba o numerze
.
Zgodnie z kryterium króla lepszy zbiór wyznacza osoba o numerze  .
.
Autor zadania: Marcin Smulewicz.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English