
Zadanie Gonitwa (gon)
Pomóż nam usprawnić bazę zadań!
Gonitwa
Limit pamięci: 32 MB
Gonitwa jest grą planszową dla dwóch osób 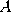 i
i  .
Plansza do gry składa się z pól ponumerowanych kolejnymi liczbami naturalnymi, poczynając od
.
Plansza do gry składa się z pól ponumerowanych kolejnymi liczbami naturalnymi, poczynając od 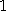 .
Dla każdej pary różnych pól wiadomo, czy są sąsiednie, czy nie.
Każdy z graczy dysponuje jednym pionem, który początkowo znajduje się na wskazanym z góry polu planszy, każdy pion na innym polu.
Ruch gracza polega na przesunięciu własnego piona na jedno z sąsiednich pól lub pozostawieniu piona na miejscu.
.
Dla każdej pary różnych pól wiadomo, czy są sąsiednie, czy nie.
Każdy z graczy dysponuje jednym pionem, który początkowo znajduje się na wskazanym z góry polu planszy, każdy pion na innym polu.
Ruch gracza polega na przesunięciu własnego piona na jedno z sąsiednich pól lub pozostawieniu piona na miejscu.
Plansza ma następujące właściwości:
- nie zawiera trójkątów, tzn. nie istnieją trzy różne pola, takie że każde dwa z nich są sąsiednie,
- każde pole może być osiągnięte zarówno przez gracza
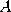 , jak i przez gracza
, jak i przez gracza 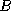 .
.
Gra składa się z wielu rund następujących po sobie.
W jednej rundzie każdy z graczy wykonuje jeden ruch, przy czym gracz 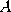 zawsze wykonuje swój ruch przed ruchem gracza
zawsze wykonuje swój ruch przed ruchem gracza 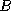 .
.
Powiemy, że gracz 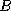 dogonił gracza
dogonił gracza 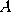 , jeżeli oba piony znajdą się na tym samym polu.
Rozstrzygnij, czy dla danych początkowych położeń obu pionów, gracz
, jeżeli oba piony znajdą się na tym samym polu.
Rozstrzygnij, czy dla danych początkowych położeń obu pionów, gracz 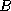 może dogonić gracza
może dogonić gracza 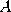 , niezależnie od tego jak dobrze gra gracz
, niezależnie od tego jak dobrze gra gracz 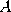 .
Jeśli tak, to po ilu rundach gracz
.
Jeśli tak, to po ilu rundach gracz 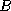 dogoni gracza
dogoni gracza 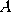 , jeżeli gracz
, jeżeli gracz 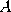 stara się uciekać jak najdłużej,
a gracz
stara się uciekać jak najdłużej,
a gracz 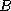 stara się dogonić gracza
stara się dogonić gracza 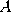 jak najszybciej i obaj grają optymalnie?
jak najszybciej i obaj grają optymalnie?
Przykład
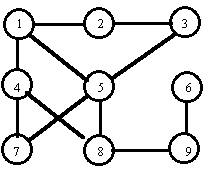
Rozważmy planszę przedstawioną na rysunku.
Sąsiednie pola planszy są połączone odcinkami.
Jeżeli na początku gry pion gracza 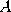 znajduje się na polu
znajduje się na polu 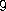 , natomiast pion gracza
, natomiast pion gracza 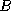 jest na polu
jest na polu  ,
to gracz
,
to gracz 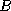 dogoni
dogoni 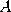 w trzeciej rundzie, o ile obaj gracze grają optymalnie.
Gdyby pion gracza
w trzeciej rundzie, o ile obaj gracze grają optymalnie.
Gdyby pion gracza 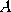 znajdował się początkowo na polu
znajdował się początkowo na polu 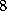 , to ruszając z pola
, to ruszając z pola  gracz
gracz 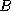 nie ma szans na dogonienie
nie ma szans na dogonienie 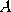 , jeżeli tylko ten gra optymalnie.
, jeżeli tylko ten gra optymalnie.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia opis planszy i numery pól, na których początkowo umieszczone są piony graczy;
- sprawdza, czy gracz
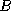 może dogonić gracza
może dogonić gracza 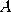 i jeżeli tak, to oblicza liczbę rund, po których
i jeżeli tak, to oblicza liczbę rund, po których 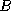 dogoni
dogoni 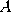 przy założeniu, że obaj gracze grają optymalnie;
przy założeniu, że obaj gracze grają optymalnie;
- zapisuje wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia znajdują się cztery liczby całkowite 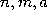 oraz
oraz 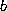 ,
oddzielone pojedynczym odstępem, gdzie:
,
oddzielone pojedynczym odstępem, gdzie: 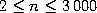 ,
, 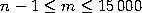 ,
, 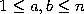 oraz
oraz 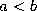 .
Są to odpowiednio: liczba pól na planszy, liczba wszystkich różnych par (nieuporządkowanych) tych pól,
które ze sobą sąsiadują, numer pola, na którym jest umieszczony pion gracza
.
Są to odpowiednio: liczba pól na planszy, liczba wszystkich różnych par (nieuporządkowanych) tych pól,
które ze sobą sąsiadują, numer pola, na którym jest umieszczony pion gracza  oraz numer pola, na którym jest umieszczony pion gracza
oraz numer pola, na którym jest umieszczony pion gracza 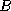 .
.
W każdym z następnych 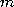 wierszy znajdują się dwie różne liczby całkowite dodatnie oddzielone pojedynczym odstępem.
Liczby w każdym z tych wierszy są numerami dwóch pól, które ze sobą sąsiadują.
wierszy znajdują się dwie różne liczby całkowite dodatnie oddzielone pojedynczym odstępem.
Liczby w każdym z tych wierszy są numerami dwóch pól, które ze sobą sąsiadują.
Wyjście
Twój program powinien zapisać w pierwszym i jedynym wierszu standardowego wyjścia jedno słowo NIE,
jeśli gracz 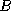 nigdy nie dogoni gracza
nigdy nie dogoni gracza 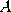 , a w przeciwnym przypadku jedną liczbę całkowitą — liczbę rund, po których, gracz
, a w przeciwnym przypadku jedną liczbę całkowitą — liczbę rund, po których, gracz  dogoni gracza
dogoni gracza  .
.
Przykład
Dla danych wejściowych:
9 11 9 4 1 2 3 2 1 4 4 7 7 5 5 1 6 9 8 5 9 8 5 3 4 8
poprawną odpowiedzią jest:
3
Autor zadania: Adam Borowski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English