
Zadanie Autobus (aut)
Pomóż nam usprawnić bazę zadań!
Autobus
Limit pamięci: 32 MB
Ulice Bajtogrodu tworzą szachownicę -
prowadzą z północy na południe, lub ze wschodu na zachód.
Ponadto każda ulica prowadzi na przestrzał przez całe miasto -
każda ulica biegnąca z północy na południe krzyżuje się z każdą ulicą
biegnącą ze wschodu na zachód i vice versa.
Ulice prowadzące z północy na południe są ponumerowane od 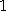 do
do  ,
w kolejności z zachodu na wschód.
Ulice prowadzące ze wschód na zachód są ponumerowane od
,
w kolejności z zachodu na wschód.
Ulice prowadzące ze wschód na zachód są ponumerowane od 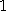 do
do 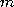 ,
w kolejności z południa na północ.
Każde skrzyżowanie
,
w kolejności z południa na północ.
Każde skrzyżowanie 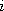 -tej ulicy biegnącej z północy na południe i
-tej ulicy biegnącej z północy na południe i
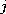 -tej ulicy biegnącej ze wschodu na zachód oznaczamy parą liczb
-tej ulicy biegnącej ze wschodu na zachód oznaczamy parą liczb
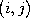 (dla
(dla 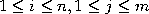 ).
).
Po ulicach Bajtogrodu kursuje autobus.
Zaczyna on trasę przy skrzyżowaniu 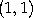 , a kończy przy
skrzyżowaniu
, a kończy przy
skrzyżowaniu 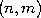 .
Ponadto autobus może jechać ulicami tylko w kierunku wschodnim
i/lub północnym.
.
Ponadto autobus może jechać ulicami tylko w kierunku wschodnim
i/lub północnym.
Przy pewnych skrzyżowaniach oczekują na autobus pasażerowie. Kierowca autobusu chce tak wybrać trasę przejazdu autobusu, aby zabrać jak najwięcej pasażerów. (Zakładamy, że bez względu na wybór trasy i tak wszyscy pasażerowie zmieszczą się w autobusie.)
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opis siatki ulic oraz liczbę pasażerów czekających przy poszczególnych skrzyżowaniach,
- obliczy ilu maksymalnie pasażerów może zabrać autobus,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu pliku wejściowego zapisane są trzy dodatnie
liczby całkowite  ,
, 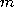 i
i 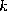 - odpowiednio: liczba ulic
biegnących z północy na południe, liczba ulic biegnących ze
wschodu na zachód i liczba skrzyżowań, przy których
pasażerowie czekają na autobus
(
- odpowiednio: liczba ulic
biegnących z północy na południe, liczba ulic biegnących ze
wschodu na zachód i liczba skrzyżowań, przy których
pasażerowie czekają na autobus
(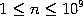 ,
, 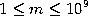 ,
, 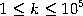 ).
).
Kolejne 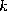 wierszy opisuje rozmieszczenie pasażerów czekających
na autobus, w jednym wierszu opisani są pasażerowie czekający
na jednym ze skrzyżowań.
W wierszu
wierszy opisuje rozmieszczenie pasażerów czekających
na autobus, w jednym wierszu opisani są pasażerowie czekający
na jednym ze skrzyżowań.
W wierszu 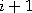 znajdują się trzy dodatnie liczby całkowite
znajdują się trzy dodatnie liczby całkowite
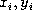 i
i 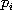 , oddzielone pojedynczymi odstępami,
, oddzielone pojedynczymi odstępami,
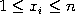 ,
, 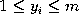 ,
, 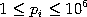 .
Taka trójka liczb oznacza, że przy skrzyżowaniu
.
Taka trójka liczb oznacza, że przy skrzyżowaniu 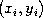 oczekuje
oczekuje 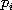 pasażerów.
Każde skrzyżowanie pojawia się w danych wejściowych co najwyżej
raz.
Łączna liczba oczekujących pasażerów nie przekracza
pasażerów.
Każde skrzyżowanie pojawia się w danych wejściowych co najwyżej
raz.
Łączna liczba oczekujących pasażerów nie przekracza
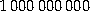 .
.
Wyjście
Twój program powinien na wyjściu wypisać jeden wiersz zawierający jedną liczbę całkowitą - maksymalną liczbę pasażerów, których może zabrać autobus.
Przykład
Dla danych wejściowych:
8 7 11 4 3 4 6 2 4 2 3 2 5 6 1 2 5 2 1 5 5 2 1 1 3 1 1 7 7 1 7 4 2 8 6 2
poprawną odpowiedzią jest:
11
W tym przypadku Twój program powinien podać wynik 11. Na poniższym rysunku zaznaczono skrzyżowania przez które przejedzie autobus zabierając 11 pasażerów.
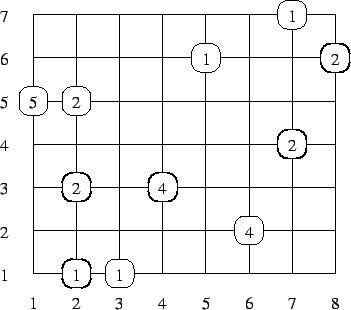
Autor zadania: Wojciech Rytter.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English