
Zadanie Rakiety (rak)
Pomóż nam usprawnić bazę zadań!
Rakiety
Limit pamięci: 32 MB
Na płaskiej mapie wyznaczono dwa rozłączne,  -elementowe zbiory punktów:
-elementowe zbiory punktów: 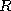 i
i 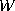 . Żadne trzy punkty ze zbioru
. Żadne trzy punkty ze zbioru 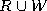 nie są współliniowe. W punktach ze zbioru
nie są współliniowe. W punktach ze zbioru 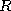 rozlokowane są rakiety typu ziemia-ziemia, natomiast w punktach ze zbioru
rozlokowane są rakiety typu ziemia-ziemia, natomiast w punktach ze zbioru 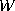 znajdują się obiekty wroga, które trzeba zniszczyć. Rakiety mogą lecieć jedynie w linii prostej, a tory rakiet nie mogą się przecinać. Chcemy dla każdej rakiety wyznaczyć cel, który powinna zniszczyć.
znajdują się obiekty wroga, które trzeba zniszczyć. Rakiety mogą lecieć jedynie w linii prostej, a tory rakiet nie mogą się przecinać. Chcemy dla każdej rakiety wyznaczyć cel, który powinna zniszczyć.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia współrzędne punktów ze zbiorów
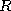 i
i 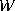 ,
, - wyznacza zbiór
 parami nie przecinających się odcinków i takich, że jeden koniec każdego odcinka należy do zbioru
parami nie przecinających się odcinków i takich, że jeden koniec każdego odcinka należy do zbioru 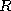 , podczas gdy drugi należy do zbioru
, podczas gdy drugi należy do zbioru 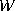 ,
, - wypisuje wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia jest zapisana jedna liczba naturalna  ,
, 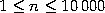 , równa liczności zbiorów
, równa liczności zbiorów 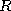 i
i 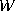 .
.
W każdym z kolejnych 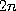 wierszy wejścia jest zapisana para liczb całkowitych z przedziału
wierszy wejścia jest zapisana para liczb całkowitych z przedziału 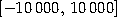 oddzielonych pojedynczym odstępem. Są to współrzędne punktu na płaszczyźnie (najpierw współrzędna
oddzielonych pojedynczym odstępem. Są to współrzędne punktu na płaszczyźnie (najpierw współrzędna  , potem współrzędna
, potem współrzędna 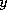 ). Pierwsze
). Pierwsze  z tych wierszy zawiera współrzędne punktów ze zbioru
z tych wierszy zawiera współrzędne punktów ze zbioru 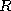 , natomiast ostatnie
, natomiast ostatnie  wierszy zawiera współrzędne punktów ze zbioru
wierszy zawiera współrzędne punktów ze zbioru 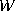 . W wierszu o numerze
. W wierszu o numerze 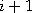 znajdują się współrzędne punktu
znajdują się współrzędne punktu 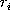 , natomiast w wierszu o numerze
, natomiast w wierszu o numerze 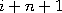 znajdują się współrzędne punktu
znajdują się współrzędne punktu 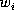 ,
, 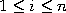 .
.
Wyjście
Standardowe wyjście powinno składać się z  wierszy. W
wierszy. W 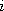 -tym wierszu należy zapisać jedną liczbę naturalną
-tym wierszu należy zapisać jedną liczbę naturalną 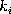 taką, że odcinek
taką, że odcinek 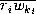 należy do wyznaczonego zbioru odcinków (innymi słowy, że rakieta z punktu
należy do wyznaczonego zbioru odcinków (innymi słowy, że rakieta z punktu 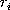 ma zniszczyć obiekt położony w punkcie
ma zniszczyć obiekt położony w punkcie 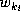 ).
).
Przykład
Dla danych wejściowych:
4 0 0 1 5 4 2 2 6 1 2 5 4 4 5 3 1
poprawną odpowiedzią jest:
2 1 4 3
Autor zadania: Wojciech Rytter.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English