
Zadanie Najlżejszy język (naj)
Pomóż nam usprawnić bazę zadań!
Najlżejszy język
Limit pamięci: 32 MB
Dany jest alfabet 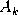 złożony z
złożony z 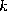 początkowych liter alfabetu angielskiego.
Każda litera w tym alfabecie ma określoną wagę, która jest dodatnią liczbą całkowitą.
Wagą słowa zbudowanego z liter alfabetu
początkowych liter alfabetu angielskiego.
Każda litera w tym alfabecie ma określoną wagę, która jest dodatnią liczbą całkowitą.
Wagą słowa zbudowanego z liter alfabetu 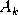 nazywamy sumę wag wszystkich jego liter.
Językiem nad alfabetem
nazywamy sumę wag wszystkich jego liter.
Językiem nad alfabetem 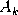 nazywamy dowolny skończony zbiór różnych słów utworzonych z liter tego alfabetu.
Wagą języka nazywamy sumę wag wszystkich jego słów.
nazywamy dowolny skończony zbiór różnych słów utworzonych z liter tego alfabetu.
Wagą języka nazywamy sumę wag wszystkich jego słów.
Mówimy że język jest bezprefiksowy, gdy żadne jego słowo nie jest prefiksem (początkiem) jego innego słowa.
Chcemy ustalić, jaka może być najmniejsza waga  -elementowego, bezprefiksowego języka nad alfabetem
-elementowego, bezprefiksowego języka nad alfabetem 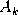 .
.
Przykład
Załóżmy, że 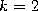 , waga litery
, waga litery  —
— 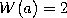 oraz waga litery
oraz waga litery 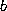 —
— 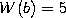 .
Wtedy: waga słowa
.
Wtedy: waga słowa 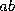 —
— 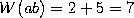 .
.
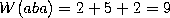 .
Waga języka
.
Waga języka 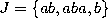 —
—  .
Język
.
Język 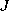 nie jest bezprefiksowy, ponieważ jego słowo
nie jest bezprefiksowy, ponieważ jego słowo 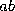 jest prefiksem słowa
jest prefiksem słowa 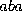 .
Najlżejszym trzyelementowym bezprefiksowym językiem nad alfabetem
.
Najlżejszym trzyelementowym bezprefiksowym językiem nad alfabetem 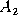 , o określonych powyżej wagach liter, jest
, o określonych powyżej wagach liter, jest 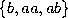 ; jego waga wynosi
; jego waga wynosi 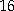 .
.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia dwie liczby naturalne
 oraz
oraz 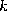 , a następnie wagi wszystkich
, a następnie wagi wszystkich 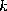 liter alfabetu
liter alfabetu 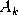 ;
;
- oblicza najmniejszą wagę bezprefiksowego
 -elementowego języka nad alfabetem
-elementowego języka nad alfabetem 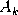 ;
;
- zapisuje wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia znajdują się dwie dodatnie liczby całkowite  i
i 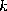 oddzielone pojedynczym odstępem
oddzielone pojedynczym odstępem 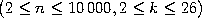 .
Są to odpowiednio: liczba słów języka i liczba liter alfabetu.
Drugi wiersz zawiera
.
Są to odpowiednio: liczba słów języka i liczba liter alfabetu.
Drugi wiersz zawiera  dodatnich liczb całkowitych nie większych niż
dodatnich liczb całkowitych nie większych niż 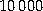 ,
oddzielonych pojedynczymi odstępami —
,
oddzielonych pojedynczymi odstępami — 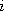 -ta liczba jest wagą
-ta liczba jest wagą 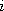 -tej litery.
-tej litery.
Wyjście
W pierwszym i jedynym wierszu standardowego wyjścia Twój program powinien wypisać jedną liczbę całkowitą —
wagę najlżejszego, bezprefiksowego,  -elementowego języka nad alfabetem
-elementowego języka nad alfabetem 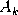 .
.
Przykład
Dla danych wejściowych:
3 2 2 5
poprawną odpowiedzią jest:
16
Autor zadania: Wojciech Rytter.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English