Wiejski listonosz

Limit pamięci: 32 MB

Wiejski listonosz musi dostarczać pocztę wszystkim mieszkańcom okolicy, którzy zamieszkują w wioskach i przy drogach łączących wioski.

Musisz pomóc listonoszowi wytyczyć trasę, która pozwoli mu przejechać wzdłuż każdej drogi i odwiedzić każdą wioskę w okolicy przynajmniej raz. Tak się szczęśliwie składa, że w rozważanych przykładach taka trasa zawsze istnieje. Jednak wytyczone trasy mogą się różnić jakością, tzn. listonosz może otrzymywać różną zapłatę za swą pracę w zależności od wybranej trasy (jak się za chwilę przekonamy, to nie zysk listonosza jest najważniejszy, a zysk jego firmy, czyli poczty). Mieszkańcy każdej wioski chcieliby, by listonosz docierał do nich jak najwcześniej. Każda wioska zawarła więc z pocztą następującą umowę: jeżeli 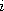-ta wioska jest odwiedzana przez listonosza jako 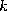-ta w kolejności (tzn. listonosz odwiedził 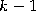różnych wiosek, zanim po raz pierwszy dotarł do wioski 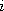) oraz 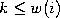, to wioska płaci poczcie 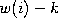euro. Jeśli jednak 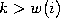, to wówczas poczta płaci wiosce 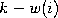euro. Ponadto poczta płaci listonoszowi jedno euro za każdy przejazd między dwiema kolejnymi wioskami na jego trasie.

W rozważanej okolicy jest wiosek, które oznaczamy liczbami naturalnymi od 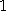do . Poczta znajduje się w wiosce oznaczonej numerem 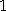, a więc trasa listonosza musi rozpoczynać się w tej wiosce. W każdej wiosce zbiega się 2, 4 lub 8 dróg. Pomiędzy dwiema wioskami może istnieć kilka różnych dróg; droga może także powracać do tej samej wioski, z której wyszła.

Zadanie

Twoim zadaniem jest napisanie programu, który:

• wczyta opis wiosek i łączących je dróg ze standardowego wejścia,
• znajdzie trasę, która prowadzi przez każdą wioskę i wzdłuż każdej drogi, i która pozwala osiągnąć poczcie maksymalny zysk (ewentualnie ponieść minimalną stratę),
• zapisze wynik na standardowym wyjściu.

Wejście

W pierwszym wierszu zapisane są dwie liczby naturalne i 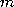, oddzielone pojedynczym odstępem; liczba (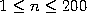) oznacza liczbę wiosek, a 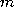jest liczbą dróg. W każdym z kolejnych wierszy znajduje się jedna liczba naturalna (dodatnia). Liczba w 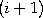-szym wierszu oznacza 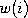(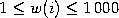), czyli wstępną kwotę płaconą poczcie przez wioskę numer 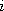(kwota ta jest oczywiście modyfikowana w opisany na początku zadania sposób). 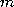W każdym z kolejnych wierszy znajdują się po dwie liczby naturalne, oddzielone pojedynczym odstępem - oznaczają one numery wiosek, które łączy kolejna droga.

Wyjście

Twój program powinien w pierwszym wierszu zapisać jedną dodatnią liczbę naturalną 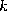. W kolejnym wierszu powinno znaleźć się 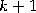liczb, oznaczających numery wiosek odwiedzanych kolejno przez listonosza w ramach optymalnej trasy.

Przykład

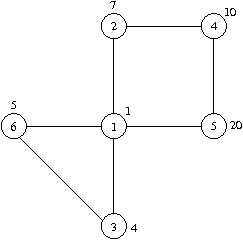
Dla danych wejściowych:

6 7
1
7
4
10
20
5
2 4
1 5
2 1
4 5
3 6
1 6
1 3

poprawną odpowiedzią jest:

7
1 5 4 2 1 6 3 1