
Zadanie Orka (ork)
Pomóż nam usprawnić bazę zadań!
Orka
Limit pamięci: 64 MB
Rolnik Bajtazar chce zaorać pole w kształcie prostokąta.
Bajtazar może zacząć od zaorania jednej skiby z dowolnego boku
pola, potem może zaorać jedną skibę z dowolnego boku niezaoranej
części pola itd., aż całe pole będzie zaorane.
Po zaoraniu każdej kolejnej skiby, niezaorana część pola
ma kształt prostokąta.
Skiby mają szerokość 1, a długość i szerokość pola wyrażają się
liczbami całkowitymi 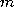 i
i  .
.
Niestety Bajtazar do orki ma tylko jedną słabowitą szkapę. Gdy szkapa zacznie orać skibę, to nie zatrzymuje się, aż zaorze ją do końca. Bajtazar musi uważać, jeżeli zaoranie skiby będzie dla szkapy zbyt wielkim wysiłkiem, to szkapa padnie. Po zaoraniu każdej kolejnej skiby szkapa może odpocząć i nabrać sił. Nie wszystkie miejsca na polu są tak samo trudne do zaorania. Bajtazar dokładnie zna swoje pole i dokładnie wie jak trudno się orze w każdym miejscu.
Podzielmy pole na 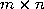 kwadratów jednostkowych.
Kwadraty będziemy identyfikować za pomocą ich współrzędnych
kwadratów jednostkowych.
Kwadraty będziemy identyfikować za pomocą ich współrzędnych
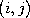 , dla
, dla 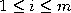 i
i 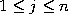 .
Każdemu z kwadratów jest przypisany jego współczynnik
trudności orki - nieujemna liczba całkowita.
Współczynnik trudności orki kwadratu o współrzędnych
.
Każdemu z kwadratów jest przypisany jego współczynnik
trudności orki - nieujemna liczba całkowita.
Współczynnik trudności orki kwadratu o współrzędnych 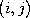 będziemy oznaczać przez
będziemy oznaczać przez 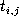 .
Dla każdej skiby suma współczynników trudności orki kwadratów
tworzących skibę nie może przekroczyć pewnej ustalonej stałej
.
Dla każdej skiby suma współczynników trudności orki kwadratów
tworzących skibę nie może przekroczyć pewnej ustalonej stałej
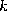 - w przeciwnym przypadku szkapa padnie.
- w przeciwnym przypadku szkapa padnie.
Bajtazar stoi przed trudnym zadaniem. Przed zaoraniem każdej skiby musi zdecydować z którego boku niezaoranej części pola ją zaorać, tak żeby szkapa nie padła. Z drugiej strony, chciałby żeby było jak najmniej skib.
Zadanie
Napisz program, który:
-
wczyta ze standardowego wejścia liczby
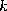 ,
, 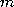 i
i  ,
oraz współczynniki trudności orki,
,
oraz współczynniki trudności orki, - wyznaczy, w jaki sposób Bajtazar powinien zaorać pole,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia znajdują się trzy
dodatnie liczby całkowite: 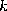 ,
, 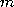 i
i  , pooddzielane
pojedynczymi odstępami,
, pooddzielane
pojedynczymi odstępami,
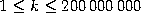 ,
,
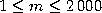 ,
,
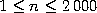 .
W kolejnych
.
W kolejnych  wierszach znajdują się współczynniki trudności
orki.
Wiersz
wierszach znajdują się współczynniki trudności
orki.
Wiersz  zawiera współczynniki
zawiera współczynniki
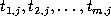 , pooddzielane pojedynczymi
odstępami,
, pooddzielane pojedynczymi
odstępami,  .
.
Wyjście
Twój program powinien wypisać na standardowe wyjście jedną liczbę całkowitą: minimalną liczbę skib powstałych po zaoraniu pola zgodnie z podanymi warunkami. Możesz założyć, że dla danych wejściowych, pole zawsze da się zaorać zgodnie z warunkami podanymi w zadaniu.
Przykład
Dla danych wejściowych:
12 6 4 6 0 4 8 0 5 0 4 5 4 6 0 0 5 6 5 6 0 5 4 0 0 5 4
poprawną odpowiedzią jest:
8

Powyższy rysunek przedstawia przykładowy sposób zaorania pola.
Autor zadania: Marcin Kubica.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English