
Zadanie Drużyny [A] (dru)
Pomóż nam usprawnić bazę zadań!
Drużyny [A]
Limit pamięci: 128 MB
Magister Bajtocki jest najbardziej lubianym nauczycielem wychowania fizycznego w Szkole Podstawowej nr 64 im. Komiwojażera Bajtazara w Bajtocji. Na każdych zajęciach, po przeprowadzeniu krótkiej rozgrzewki, pyta uczniów w jaką grę zespołową chcieliby grać, a następnie pomaga im podzielić się na drużyny.
Podczas zbiórki uczniowie ustawiają się w szereg, numerując się
tym samym kolejnymi liczbami od 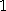 do
do  .
Mgr Bajtocki tworzy drużyny tak, aby każda z nich stanowiła
spójny fragment szeregu.
Każdy z uczniów musi należeć do jednej z drużyn.
.
Mgr Bajtocki tworzy drużyny tak, aby każda z nich stanowiła
spójny fragment szeregu.
Każdy z uczniów musi należeć do jednej z drużyn.
Nauczyciel dobrze zna swoich uczniów i wie, że uczeń o numerze 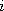 będzie zadowolony z podziału tylko wtedy,
gdy liczba zawodników w jego drużynie będzie nie mniejsza niż
będzie zadowolony z podziału tylko wtedy,
gdy liczba zawodników w jego drużynie będzie nie mniejsza niż 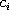 oraz
nie większa niż
oraz
nie większa niż 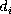 .
.
Mgr Bajtocki zastanawia się, czy da się podzielić uczniów na drużyny tak, aby każdy z nich był zadowolony. Jeśli jest to możliwe, chciałby poznać maksymalną możliwą liczbę powstałych drużyn, a także liczbę podziałów realizujących to maksimum.
Wejście
W pierwszym wierszu wejścia znajduje się jedna liczba całkowita  (
(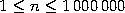 ), oznaczająca liczbę uczniów.
Kolejne
), oznaczająca liczbę uczniów.
Kolejne  wierszy opisuje preferencje uczniów:
wierszy opisuje preferencje uczniów: 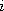 -ty z tych wierszy zawiera
dwie liczby całkowite
-ty z tych wierszy zawiera
dwie liczby całkowite 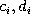 (
(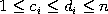 ), oznaczające,
że uczeń o numerze
), oznaczające,
że uczeń o numerze 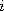 będzie zadowolony,
gdy liczba zawodników w jego drużynie będzie należała do przedziału
będzie zadowolony,
gdy liczba zawodników w jego drużynie będzie należała do przedziału 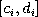 .
.
Wyjście
Jeśli da się podzielić uczniów według procedury mgra Bajtockiego
tak, aby każdy z nich był zadowolony, na wyjście należy
wypisać dwie liczby całkowite oddzielone pojedynczym odstępem - maksymalną liczbę drużyn i
liczbę podziałów realizujących to maksimum.
Drugą z tych liczb należy wypisać modulo 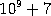 .
.
Jeśli uczniów nie da się podzielić zgodnie z powyższymi wymogami, na wyjście należy wypisać słowo NIE.
Przykład
Dla danych wejściowych:
9 1 4 2 5 3 4 1 5 1 1 2 5 3 5 1 3 1 1
poprawną odpowiedzią jest:
5 2
natomiast dla danych wejściowych:
2 1 1 2 2
poprawnym wynikiem jest:
NIE
Autor zadania: Adam Karczmarz.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English