
Zadanie Mecze [B] (mec)
Pomóż nam usprawnić bazę zadań!
Mecze [B]
Limit pamięci: 128 MB
W sobotnie przedpołudnie na boisku Klubu Sportowego "Bajtusie" zbierze się  chłopców.
Szczęśliwie się złożyło, że liczba chłopców jest parzysta.
Dzięki temu wszyscy chłopcy będą mogli radośnie spędzić ten sobotni dzień, grając w piłkę.
chłopców.
Szczęśliwie się złożyło, że liczba chłopców jest parzysta.
Dzięki temu wszyscy chłopcy będą mogli radośnie spędzić ten sobotni dzień, grając w piłkę.
Bajtazar jest trenerem klubu i to on jest odpowiedzialny za dobór składów na poszczególne mecze. Bajtazar wie, że chłopcy bardzo lubią współzawodniczyć, dlatego też postanowił w taki sposób ułożyć składy drużyn, aby każdych dwóch chłopców miało szansę zagrać przeciwko sobie w jakimś meczu (tzn. choć raz zagrać w przeciwnych drużynach).
Biorąc pod uwagę umiejętności chłopców, Bajtazar zaproponował już składy
drużyn na najbliższe  meczów.
W każdym meczu zagrają wszyscy chłopcy, podzieleni na dwie drużyny po
meczów.
W każdym meczu zagrają wszyscy chłopcy, podzieleni na dwie drużyny po  zawodników.
Pomóż Bajtazarowi stwierdzić, czy każda para chłopców zagra przeciwko sobie
choć w jednym z zaplanowanych meczów.
zawodników.
Pomóż Bajtazarowi stwierdzić, czy każda para chłopców zagra przeciwko sobie
choć w jednym z zaplanowanych meczów.
Wejście
W pierwszym wierszu wejścia znajdują się dwie liczby całkowite  oraz
oraz  (
( ,
,  ) oznaczające liczbę chłopców oraz
liczbę zaplanowanych meczów.
Każdy chłopiec ma na koszulce napisany numer - liczbę całkowitą między
) oznaczające liczbę chłopców oraz
liczbę zaplanowanych meczów.
Każdy chłopiec ma na koszulce napisany numer - liczbę całkowitą między  a
a  .
Numery na koszulkach poszczególnych chłopców są parami różne.
.
Numery na koszulkach poszczególnych chłopców są parami różne.
Każdy z kolejnych 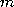 wierszy zawiera po
wierszy zawiera po  parami różnych liczb całkowitych
z zakresu od
parami różnych liczb całkowitych
z zakresu od  do
do  opisujących składy drużyn na poszczególne mecze.
Pierwsze
opisujących składy drużyn na poszczególne mecze.
Pierwsze  liczb w każdym wierszu to numery zawodników grających
w pierwszej drużynie, a drugie
liczb w każdym wierszu to numery zawodników grających
w pierwszej drużynie, a drugie  liczb - numery zawodników
wchodzących w skład drugiej drużyny.
liczb - numery zawodników
wchodzących w skład drugiej drużyny.
Wyjście
Twój program powinien wypisać na wyjście jedno słowo TAK lub NIE, w zależności od tego, czy każda para chłopców zagra przeciwko sobie co najmniej w jednym meczu, czy też nie.
Przykład
Dla danych wejściowych:
6 3 4 6 1 3 5 2 1 4 5 2 3 6 1 2 6 4 5 3
poprawną odpowiedzią jest:
TAK
natomiast dla danych wejściowych:
6 3 4 6 1 3 5 2 1 4 5 2 3 6 1 2 3 4 5 6
poprawnym wynikiem jest:
NIE
Wyjaśnienie do przykładu: W pierwszym przykładzie każda para zawodników gra w przeciwnych drużynach w jednym meczu (np. zawodnicy o numerach 1 i 6), w dwóch meczach (np. zawodnicy 1 i 2) lub nawet we wszystkich trzech meczach (np. zawodnicy 1 i 3). W drugim przykładzie zawodnicy o numerach 2 i 3 zawsze grają w tej samej drużynie.
Autorzy zadania: Tomasz Idziaszek, Jakub Łącki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English