
Zadanie Nieokiełzane drzewo (nie)
Pomóż nam usprawnić bazę zadań!
Nieokiełzane drzewo
Limit pamięci: 32 MB
Bajtazar prosi Cię o pomoc przy obrabianiu pewnego drzewa  . Jest to
drzewo binarne, którego liście mają pewne etykiety (etykiety mogą się
powtarzać). Dla każdej etykiety
. Jest to
drzewo binarne, którego liście mają pewne etykiety (etykiety mogą się
powtarzać). Dla każdej etykiety  Bajtazar chciałby zobaczyć drzewo
Bajtazar chciałby zobaczyć drzewo  o następujących własnościach:
o następujących własnościach:
- liśćmi drzewa
 są te liście drzewa
są te liście drzewa 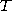 , które mają etykietę
, które mają etykietę
 ,
,
- do drzewa
 bierzemy te wierzchołki wewnętrzne drzewa
bierzemy te wierzchołki wewnętrzne drzewa  , których oba
poddrzewa (tzn. lewe i prawe) zawierają etykietę
, których oba
poddrzewa (tzn. lewe i prawe) zawierają etykietę  ,
,
- dwa wierzchołki drzewa
 łączymy krawędzią, jeśli w drzewie
łączymy krawędzią, jeśli w drzewie  istnieje między nimi ścieżka nie przechodząca przez żaden inny wierzchołek
wzięty do drzewa
istnieje między nimi ścieżka nie przechodząca przez żaden inny wierzchołek
wzięty do drzewa  .
.
Pomóż Bajtazarowi i napisz program, który dla każdej etykiety  występującej w drzewie
występującej w drzewie  wyznaczy drzewo
wyznaczy drzewo  .
.
Zadanie
Napisz program, który:
-
wczyta ze standardowego wejścia opis drzewa
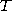 ,
,
-
dla każdej etykiety
 występującej w drzewie
występującej w drzewie  wyznaczy drzewo
wyznaczy drzewo  ,
,
- wypisze opisy tych drzew na standardowe wyjście.
Wejście
W każdym wierszu standardowego wejścia opisany jest dokładnie jeden
wierzchołek drzewa  . Drzewo to jest zapisane w kolejności pre-order.
W pierwszym wierszu opisu drzewa (zarówno całego, jak i każdego poddrzewa)
znajduje się opis korzenia, następnie (jeśli korzeń nie
jest liściem) opis lewego poddrzewa, po czym opis prawego poddrzewa.
Jeśli mamy do czynienia z wierzchołkiem wewnętrznym, w wierszu znajduje
się pojedyńczy znak gwiazdki '*'. W przypadku liścia, w wierszu znajduje
się jego etykieta. Jest to niepusty napis, który może zawierać
wyłącznie małe litery od 'a' do 'z'. Łączna długość
wszystkich etykiet będzie nie większa niż
. Drzewo to jest zapisane w kolejności pre-order.
W pierwszym wierszu opisu drzewa (zarówno całego, jak i każdego poddrzewa)
znajduje się opis korzenia, następnie (jeśli korzeń nie
jest liściem) opis lewego poddrzewa, po czym opis prawego poddrzewa.
Jeśli mamy do czynienia z wierzchołkiem wewnętrznym, w wierszu znajduje
się pojedyńczy znak gwiazdki '*'. W przypadku liścia, w wierszu znajduje
się jego etykieta. Jest to niepusty napis, który może zawierać
wyłącznie małe litery od 'a' do 'z'. Łączna długość
wszystkich etykiet będzie nie większa niż  (każdą etykietę
liczymy tyle razy, ile występuje na wejściu).
(każdą etykietę
liczymy tyle razy, ile występuje na wejściu).
Wierzchołki drzewa numerowane są zgodnie z ich kolejnością występowania na wejściu, poczynając od 1 (czyli numer wierzchołka równa się numerowi wiersza).
Wyjście
Twój program powinien wypisać na standardowym wyjściu opisy
wszystkich drzew  , w kolejności leksykograficznej etykiet.
Opis każdego drzewa powinien mieścić się w jednym wierszu. Podobnie jak na
wejściu ma to być opis pre-order, jednak wypisywać należy numery
wierzchołków, które są w drzewie. Zatem opis drzewa to numer korzenia,
po czym (jeśli to nie liść) opisy lewego i prawego poddrzewa.
, w kolejności leksykograficznej etykiet.
Opis każdego drzewa powinien mieścić się w jednym wierszu. Podobnie jak na
wejściu ma to być opis pre-order, jednak wypisywać należy numery
wierzchołków, które są w drzewie. Zatem opis drzewa to numer korzenia,
po czym (jeśli to nie liść) opisy lewego i prawego poddrzewa.
Przykład
Dla danych wejściowych:
* * a ab * * c ab * c c

poprawną odpowiedzią jest:
3 1 4 8 5 7 9 10 11

Autor zadania: Paweł Parys.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English