
Zadanie Automorfizmy [B] (aut)
Pomóż nam usprawnić bazę zadań!
Automorfizmy [B]
Limit pamięci: 128 MB
Drzewem nazywamy graf nieskierowany, w którym każde dwa wierzchołki są połączone dokładnie jedną ścieżką prostą, czyli ścieżką bez powtarzających się wierzchołków.
Rozważmy  -wierzchołkowe drzewo, w którym wierzchołki są ponumerowane od 1
do
-wierzchołkowe drzewo, w którym wierzchołki są ponumerowane od 1
do  .
Niech
.
Niech 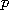 będzie dowolną permutacją zbioru wierzchołków tego drzewa (czyli
funkcją różnowartościową
będzie dowolną permutacją zbioru wierzchołków tego drzewa (czyli
funkcją różnowartościową 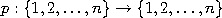 ).
Permutację
).
Permutację 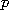 nazywamy automorfizmem, jeżeli dla dowolnych dwóch
wierzchołków
nazywamy automorfizmem, jeżeli dla dowolnych dwóch
wierzchołków 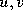 drzewa, wierzchołki
drzewa, wierzchołki 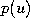 i
i 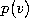 są połączone krawędzią
wtedy i tylko wtedy, gdy wierzchołki
są połączone krawędzią
wtedy i tylko wtedy, gdy wierzchołki  i
i  są połączone krawędzią.
są połączone krawędzią.
W tym zadaniu interesuje nas liczba automorfizmów danego drzewa, a dokładniej,
reszta z dzielenia tej liczby przez 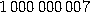 .
.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się jedna liczba całkowita  (
(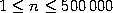 ), oznaczająca liczbę wierzchołków drzewa.
Każdy z kolejnych
), oznaczająca liczbę wierzchołków drzewa.
Każdy z kolejnych 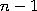 wierszy zawiera dwie liczby całkowite
wierszy zawiera dwie liczby całkowite 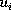 i
i 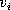 (
(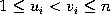 ), reprezentujące krawędź łączącą wierzchołki
), reprezentujące krawędź łączącą wierzchołki
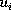 i
i 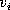 .
.
Wyjście
W pierwszym i jedynym wierszu standardowego wyjścia Twój program powinien wypisać jedną
liczbę całkowitą: resztę z dzielenia liczby automorfizmów wyjściowego drzewa
przez 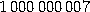 .
.
Przykład
Dla danych wejściowych:
6 1 3 2 3 3 4 4 5 4 6
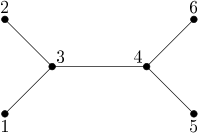
poprawną odpowiedzią jest:
8
Wyjaśnienie do przykładu: Przedstawione drzewo ma 8 automorfizmów. Trzy przykładowe z nich to:
-
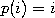 dla
dla 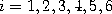
-
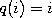 dla
dla 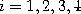 ,
, 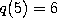 ,
, 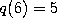
-
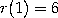 ,
, 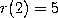 ,
, 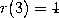 ,
, 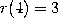 ,
, 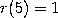 ,
, 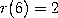 .
.
Autor zadania: Adam Malinowski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English